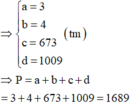Cho a,b,c,d là số nguyên biết a+b=c+d và c*d là các số nguyên liên tiếp .CMR c=d
NH
Những câu hỏi liên quan
Cho đa Thức P(x) có các hệ số đều là số nguyên và a,b,c,d là bốn số nguyên lẻ phân biệt thỏa mãn P(a)=P(d)=-1,P(b)=P(c)=3 .Biết rằng a>b>c chứng minh rằng a,b,c,d là bốn số nguyên lẻ liên tiếp (theo 1 thứ tự nào đó )
Sử dụng quy tắc đa thức: \(P\left(a\right)-P\left(b\right)\) chia hết \(a-b\) cho đa thức hệ số nguyên
Do a;b;c;d lẻ nên hiệu của chúng đều chẵn
\(P\left(c\right)-P\left(a\right)=4\Rightarrow4⋮c-a\Rightarrow\left[{}\begin{matrix}c-a=-2\\c-a=-4\end{matrix}\right.\)
Tương tự ta có \(\left[{}\begin{matrix}b-a=-2\\b-a=-4\end{matrix}\right.\)
Mà \(a>b>c\) \(\Rightarrow b-a>c-a\Rightarrow\left[{}\begin{matrix}b-a=-2\\c-a=-4\end{matrix}\right.\)
\(\Rightarrow a;b;c\) là 3 số nguyên lẻ liên tiếp
Lại có \(P\left(b\right)-P\left(d\right)=4⋮b-d\Rightarrow b-d=\left\{-4;-2;2;4\right\}\)
Tương tự: \(c-d=\left\{-4;-2;2;4\right\}\) (1)
Do đã chứng minh được a; b và c là 2 số lẻ liên tiếp \(\Rightarrow c=b-2\) ; \(c=a-4\) (2)
- Nếu \(b-d=-4\Rightarrow c-d=b-2-d=-4-2=-6\) không thỏa mãn (1) (loại)
- Nếu \(b-d=-2\Rightarrow c-d=b-d-2=-4\) \(\Rightarrow c=d-4\)
\(\Rightarrow d=a\) theo (2) trái giả thiết a;b;c;d phân biệt (loại)
- Nếu \(b-d=2\Rightarrow c-d=b-d-2=0\Rightarrow c=d\) trái giả thiết c;d phân biệt (loại)
- Nếu \(b-d=4\Rightarrow c-d=b-d-2=2\)
\(\Rightarrow d\) là số lẻ liền trước của c
Vậy a;b;c;d là bốn số nguyên lẻ liên tiếp theo thứ tự \(a>b>c>d\)
Đúng 4
Bình luận (0)
Cho f(x) là đa thức hệ số nguyên a,b,c,d mà a<b,f(a)=f(b)=1;c<d;f(c)=f(d)=-1,a<c.Chứng minh a,b,c,d là 4 số nguyên liên tiếp
bạn ơi mình nghĩ là đâu thể gọi dạng của f(x) được ?
Cho các số nguyên a,b,c,d. Biết ab là số liền sau của cd và a+b = c+d
CMR a và b bằng nhau
Cho tứ giác ABCD có số đo các cạnh là a,b,c,d (a,b,c,d là các số nguyên dương). Biết a,b,c,d đều là các ước của a+b+c+d. CMR: tứ giác ABCD có ít nhất hai cạnh bằng nhau.
- Cho a,b,c,d là các số nguyên bất kỳ. CMR: (a-b)(a-c)(a-d)(b-c)(b-d)(c-d) chia hết cho 12
tham khảo đỡ đi:
https://olm.vn/hoi-dap/detail/20065386691.html
Đúng 2
Bình luận (0)
Xem thêm câu trả lời
1)tìm 3 số nguyên liên tiếp biết a2+b2+c2 cũng là số nguyên tố
2)a2+b2=c2+d2.CMR a+b+c+d là hợp số
3)a2+b2+c2+d2+e2=g2
CMR abcdeg chẵn
2) \(a^2+b^2=c^2+d^2\)
\(\Leftrightarrow\left(a+b\right)^2-2ab=\left(c+d\right)^2-2cd\)
\(\Leftrightarrow\left(a+b\right)^2-\left(c+d\right)^2=2\left(ab-cd\right)\)
\(\Leftrightarrow\left(a+b+c+d\right)\left(a+b-c-d\right)=2\left(ab-cd\right)\)
Ta có \(\left(a+b+c+d\right)+\left(a+b-c-d\right)=2\left(a+b\right)\) là số chẵn
\(\Rightarrow\) \(\left(a+b+c+d\right)\) và \(\left(a+b-c-d\right)\) có cùng tính chẵn lẻ
Mặt khác \(\left(a+b+c+d\right)\left(a+b-c-d\right)=2\left(ab-cd\right)\) chia hết cho 2
Nên \(\left(a+b+c+d\right)\) và \(\left(a+b-c-d\right)\) ko thể cùng lẻ
\(\Rightarrow\) \(\left(a+b+c+d\right)\) và \(\left(a+b-c-d\right)\) cùng chẵn
Mà \(a+b+c+d>2\) nên \(a+b+c+d\) là hợp số.
Đúng 0
Bình luận (0)
Cho a, b là hai số nguyên sao cho tồn tại hai số nguyên liên tiếp c và d để a - b = a2c - b2d. Chứng minh |a - b| là số chính phương.
Cho các số nguyên a,b,c,d biết rằng a-d=c-b và ab+1=cd. CMR: c=d
Cho hàm số
f
x
ln
1
−
1
x
2
.
Biết rằng
f
2
+
F
3
+
...
+
f
2018
ln
a
−
ln
b
+
ln
c...
Đọc tiếp
Cho hàm số f x = ln 1 − 1 x 2 . Biết rằng f 2 + F 3 + ... + f 2018 = ln a − ln b + ln c − ln d với a, b, c, d là các số nguyên dương, trong đó a, c, d là các số nguyên tố và a < b < c < d . . Tính P = a + b + c + d .
A. 1986
B. 1698
C. 1689
D. 1968



 #hoktot#
#hoktot#