Cho tập A = { x ∈ Z / -3 ≤ x <3 }.Tính tổng của các phần tử A
AP
Những câu hỏi liên quan
Cho hai tập hợp:
\(A = \{ x \in \mathbb{Z}| - 3 < x < 3\} ,\)\(B = \{ x \in \mathbb{Z}| - 3 \le x \le 3\} \)
a) Viết tập hợp A, B bằng cách liệt kê các phần tử của tập hợp.
b) Mỗi phần tử của tập hợp A có thuộc tập hợp B không?
a) \(A = \{ - 2; - 1;0;1;2\} \)
\(B = \{ - 3; - 2; - 1;0;1;2;3\} \)
b) Mỗi phần tử của tập hợp A đều thuộc tập hợp B.
Đúng 0
Bình luận (0)
Cho tập A = {x thuộc z|x^2/2x+3 thuộc z} số tập con của A là
Để \(\dfrac{x^2}{2x+3}\in Z\) thì \(x^2⋮2x+3\)
=>\(4x^2⋮2x+3\)
=>\(4x^2-9+9⋮2x+3\)
=>\(2x+3\inƯ\left(9\right)\)
=>\(2x+3\in\left\{1;-1;3;-3;9;-9\right\}\)
=>\(2x\in\left\{-2;-4;0;-6;6;-12\right\}\)
=>\(x\in\left\{-1;-2;0;-3;3;-6\right\}\)
=>A={-1;-2;0;-3;3;-6}
Số tập con của A là \(2^6=64\left(tập\right)\)
Đúng 0
Bình luận (0)
Cho tập A={x thuộc Z|x^2/2x+3 thuộc Z} số tập con của A là
Cho 2 tập hợp A = {x là con Z ! x > -4 } , B = {x là con Z ! < 3 } . Viết tập hợp A giao B bằng 2 cách.
Cho tập
A
x
∈
Z
|
-
1
≤
x
≤
5
. Số tập con gồm 3 phần tử của A là A.
C
7
3
B.
C
6
3
C.
C
8
3
D. ...
Đọc tiếp
Cho tập A = x ∈ Z | - 1 ≤ x ≤ 5 . Số tập con gồm 3 phần tử của A là
A. C 7 3
B. C 6 3
C. C 8 3
D. C 5 3
Cho `2` tập hợp `A={x in Z` | `x > m }` và `B= {x in Z ` | ` x <= (2m-1)/3}` với `m in Z`. TÌm `m` để \(A\cap B\)
\(A\cap B=\left\{{}\begin{matrix}x>m\\x\le\dfrac{2m-1}{3}\end{matrix}\right.\left(1\right)\)
\(TH1:m< \dfrac{2m-1}{3}\)
\(\Leftrightarrow m-\dfrac{2m-1}{3}< 0\)
\(\Leftrightarrow\dfrac{m-1}{3}< 0\)
\(\Leftrightarrow m< 1\)
\(\left(1\right)\Leftrightarrow A\cap B=\left\{x\in Z|m< x\le\dfrac{2m-1}{3}\right\}\)
\(TH2:m>\dfrac{2m-1}{3}\)
\(\Leftrightarrow m-\dfrac{2m-1}{3}>0\)
\(\Leftrightarrow\dfrac{m-1}{3}>0\)
\(\Leftrightarrow m>1\)
\(\left(1\right)\Leftrightarrow A\cap B=\varnothing\)
Đúng 1
Bình luận (1)
Cho \(A = \left\{ {x \in \mathbb{Z}|\;x < 4} \right\},\) \( \,B = \left\{ {x \in \mathbb{Z}|\;\left( {5x - 3{x^2}} \right)\left( {{x^2} + 2x - 3} \right) = 0} \right\}\)
a) Liệt kê các phần tử của hai tập hợp A và B.
b) Hãy xác định các tập hợp \(A \cap B,A \cup B\) và \(A\,{\rm{\backslash }}\,B\)
a) \(A = \{ 3;2;1;0; - 1; - 2; - 3; -4; ...\} \)
Tập hợp B là tập các nghiệm nguyên của phương trình \(\left( {5x - 3{x^2}} \right)\left( {{x^2} + 2x - 3} \right) = 0\)
Ta có:
\(\begin{array}{l}\left( {5x - 3{x^2}} \right)\left( {{x^2} + 2x - 3} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}5x - 3{x^2} = 0\\{x^2} + 2x - 3 = 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}\left[ \begin{array}{l}x = 0\\x = \frac{5}{3}\end{array} \right.\\\left[ \begin{array}{l}x = 1\\x = - 3\end{array} \right.\end{array} \right.\end{array}\)
Vì \(\frac{5}{3} \notin \mathbb Z\) nên \(B = \left\{ { - 3;0;1} \right\}\).
b) \(A \cap B = \left\{ {x \in A|x \in B} \right\} = \{ - 3;0;1\} = B\)
\(A \cup B = \) {\(x \in A\) hoặc \(x \in B\)} \( = \{ 3;2;1;0; - 1; - 2; - 3;...\} = A\)
\(A\,{\rm{\backslash }}\,B = \left\{ {x \in A|x \notin B} \right\} = \{ 3;2;1;0; - 1; - 2; - 3;...\} {\rm{\backslash }}\;\{ - 3;0;1\} = \{ 3;2; - 1; - 2; - 4; - 5; - 6;...\} \)
Đúng 0
Bình luận (0)
Cho tập hợp A = x ∈ Z : − 3 ≤ x ≤ 3 . Số phần tử của A bằng:
A. 7
B. 6
C. 8
D. 5
Đáp án A
Phương pháp: Liệt kê các phần tử của tập A
Cách giải:
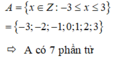
Đúng 0
Bình luận (0)
Cho tập hợp A
x
∈
Z
:
-
3
≤
x
≤
3
. Số phần tử của A bằng: A. 7 B. 6 C. 8 D. 5
Đọc tiếp
Cho tập hợp A = x ∈ Z : - 3 ≤ x ≤ 3 . Số phần tử của A bằng:
A. 7
B. 6
C. 8
D. 5
Đáp án A
Phương pháp: Liệt kê các phần tử của tập A
Cách giải:
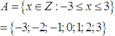
=> A có 7 phần tử
Đúng 0
Bình luận (0)






