Cho hình vẽ sau. Hãy chứng minh
a) ∆ABC = ∆ADB
b) Chứng minh BC = BD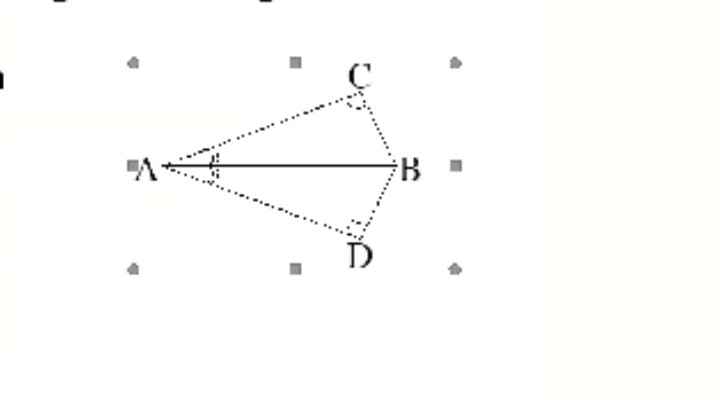
BT
Những câu hỏi liên quan
Bài 10: Cho ∆ABC vuông tại A. Vẽ đường cao AH. Trên cạnh BC lấy điểm D sao cho BD = BA a) Chứng minh: góc BAD = góc ADB b) Chứng minh: AD là phân giác của góc HAC c) Vẽ DK vuông góc AC ( K thuộc AC). Chứng minh: AK = AH d) Chứng minh: AB + AC < BC + AH
Cho tam giác ABC vuông tại A. Vẽ đường cao AH. Trên cạnh BC lấy điểm D sao cho BD=BA
a, Chứng minh góc BAD = góc ADB
b, Chứng minh AD là phân giác của góc HAC
c, Vẽ DK vuông góc AC (K thuộc AC). Chứng minh AK = AH
b17
a: BA=BD
=>ΔBAD cân tại B
=>góc BAD=góc BDA
b: góc HAD+góc BDA=90 độ
góc CAD+góc BAD=90 độ
mà góc BAD=góc BDA
nên góc HAD=góc CAD
=>AD là phân giác của góc HAC
c: Xét ΔADH vuông tại H và ΔADK vuông tại K có
AD chung
góc HAD=góc KAD
=>ΔADH=ΔADK
=>AH=AK
Đúng 4
Bình luận (0)
bài giải nè ! ![]()
a: BA=BD
=>ΔBAD cân tại B
=>góc BAD=góc BDA
b: góc HAD+góc BDA=90 độ
góc CAD+góc BAD=90 độ
mà góc BAD=góc BDA
nên góc HAD=góc CAD
=>AD là phân giác của góc HAC
c: Xét ΔADH vuông tại H và ΔADK vuông tại K có
AD chung
góc HAD=góc KAD
=>ΔADH=ΔADK
=>AH=AK
Đúng 1
Bình luận (1)
Cho tam giác nhọn ABC các đường cao BD CE cắt nhau ở H chứng minh rằng. a. tam giác AEC đồng dạng tam giác ADB b. Kẻ HK vuông góc với BC ( k thuộc BC) chứng minh BH×BD=BK×BC Cho mình xin cả hình nha
a: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
góc A chung
=>ΔADB đồng dạng với ΔAEC
b: Xét ΔBKH vuông tại K và ΔBDC vuông tại D có
góc KBH chung
=>ΔBKH đồng dạng với ΔBDC
=>BK/BD=BH/BC
=>BK*BC=BD*BH
Đúng 1
Bình luận (0)
Hình học lớp 8
Cho tam giác ABC có 3 góc nhọn. Vẽ hai đường cao BD và CE (D thuộc AC, E thuộc AB)
a) Chứng minh: Tam giác ADB đồng dạng tam giác AEC
b) Chứng minh: AD. AC = AB.AE
c) Biết DE= 2cm, BC = 4cm. Tính diện tích ADE/ diện tích ABC
(Mai thi rồi cíu tôi đi 💦) 
a, Xét tam giác ADB và tam giác AEC có
^ADB = ^AEC = 900
^DAB _ chung
Vậy tam giác ADB ~ tam giác AEC (g.g)
b, \(\dfrac{AD}{AE}=\dfrac{AB}{AC}\Rightarrow AD.AC=AB.AE\)
c, \(\dfrac{S_{ADE}}{S_{ABC}}=\left(\dfrac{DE}{BC}\right)^2=\dfrac{1}{4}\)
Đúng 2
Bình luận (1)
cho tam giác ABC vuông tại A. vẽ đường cao AH. trên cạnh BC lấy điểm D sao cho BD=BA.
a, chứng minh góc BAD= góc ADB
b, chứng minh AD là phân giác của góc HAD
c, vẽ DK vuông góc với AC( K thuộc AC). chứng minh AK=AH
d, chứng minh AB+AC< BC+2AH
Cho tam giác ABC vuông tại A. Vẽ đường cao AH.Trên cạnh BC lấy điểm D sao cho BD = BA
a, chứng minh: góc BAD = góc ADB
b, Chứng minh: AD là phân giác của góc HAC
c, Vẽ DK vuông góc AC ( K thuộc AC). Chứng minh: AK = AH
d, Chứng minh : AB + AC < BC + 2AH
Cho tam giác ABC có góc A bằng 90 độ. Đường thẳng AH vuông góc với BC tại H.Trên BC lấy D sao cho BD=BA
a, Chứng minh : Góc BAD = góc ADB
b, Chứng minh : AD là phân giác của góc HAD
c, Vẽ DK vuông góc AC ( K\(\in\)AC) . Chứng minh AH=AK
d, AB+AC < BC+2AH
a) Xét ΔBAD có BA=BD(gt)
nên ΔBAD cân tại B(Định nghĩa tam giác cân)
Suy ra: \(\widehat{BAD}=\widehat{BDA}\)(hai góc ở đáy)
b) Ta có: \(\widehat{CAD}+\widehat{BAD}=90^0\)(tia AD nằm giữa hai tia AB,AC)
\(\widehat{HAD}+\widehat{HDA}=90^0\)(ΔHAD vuông tại H)
mà \(\widehat{BAD}=\widehat{HDA}\)(cmt)
nên \(\widehat{CAD}=\widehat{HAD}\)
hay AD là tia phân giác của \(\widehat{HAD}\)
c) Xét ΔAHD vuông tại H và ΔAKD vuông tại K có
AD chung
\(\widehat{HAD}=\widehat{KAD}\)(AD là tia phân giác của \(\widehat{HAK}\))
Do đó: ΔAHD=ΔAKD(Cạnh huyền-góc nhọn)
Suy ra: AH=AK(hai cạnh tương ứng)
Đúng 1
Bình luận (0)
cho tam giác ABC vuông tại A. Vẽ đường cao AH.Trên cạnh BC lấy điểm D sao cho BD=BD
a, Chứng minh ; góc BAD=góc ADB
b, Chứng minh AS là tia phân giác của góc HAC
c,Vẽ DK vuông góc AC (K thuộc AC).C/M AK=AH
d,chứng minh ; AB + AC <BC+ 2AH
Cho ΔABC vuông tại A, vẽ đường cao AH. Trên BC lấy D sao cho BD=BA
a, Chứng minh ∠BAD = ∠ADB
b, Chứng minh: AD là phân giác của ∠HAC
c, Vẽ DK ⊥ AC ( K∈ AC) Chứng minh: AK= AH
d, Chứng minh: AB+AC<BC+2AH
a) ΔBAD có : BA = BD
\(\Rightarrow\) ΔBAD cân tại B
\(\Rightarrow\) \(\widehat{BAD}\) = \(\widehat{BDA}\)
b) ΔABC có : \(\widehat{A}\) = 90\(^O\)
\(\Rightarrow\) \(\widehat{BAD}\) + \(\widehat{DAC}\) = 90\(^O\)
ΔHAD có : \(\widehat{H}\) = 90\(^O\)
\(\Rightarrow\) \(\widehat{HAD}\) + \(\widehat{HDA}\) = 90\(^O\)
\(\Rightarrow\) \(\widehat{BAD}\) + \(\widehat{DAC}\) = \(\widehat{HAD}\) + \(\widehat{HDA}\) ( = 90\(^O\) )
mà \(\widehat{BAD}\) = \(\widehat{HDA}\) ( CMT ) \(\Rightarrow\) \(\widehat{DAC}\) = \(\widehat{HAD}\)
\(\Rightarrow\) AD là phân giác của \(\widehat{HAC}\)
c) Xét ΔAHD và ΔAKD có :
\(\widehat{AHD}\) = \(\widehat{AKD}\) = 90\(^O\)
AD chung
\(\widehat{HAD}\) = \(\widehat{KAD}\) ( AD là phân giác của \(\widehat{HAC}\) )
\(\Rightarrow\) Δvuông AHD = Δvuông AKD ( cạnh huyền - góc nhọn )
\(\Rightarrow\) AH = AK ( hai cạnh tương ứng )
d) AB + AC = AB + AK + KC
BC + 2AH = BD + DC + 2AH
mà AB = BD (GT)
AK = AH (CMT) \(\Rightarrow\) AK < 2AH
KC < DC ( quan hệ giữa đường xiên và đường vuông góc )
\(\Rightarrow\) AB + AC < BC + 2AH
Đúng 0
Bình luận (0)
b) Câu a bạn kia giải rồi câu B mink còn cách ngắn hơn nè
Ta có : ^BAH+^HAD=^BAD (câu a)
Mà ^ADB=^DAC+^C
\(\Rightarrow\)^BAH+^HAD=^DAC+^C (1)
Xét tam giác vuông BAC có
^B+^C=90\(^0\)
Ta có ^HAB=^BAH+^B= \(90^0\)
\(\Rightarrow\)^B+^C = ^BAH+^B \(\Rightarrow\)^C=^BAH
Từ (1) và (2)
\(\Rightarrow\)^HAD = ^DAC
Đúng 0
Bình luận (0)
Xét tam giác BAH có
AH+HB>AB (BĐT trong tam giác) (1)
Xét tam giác HAC có
AH+HC>AC (BĐT trong tam giac) (2)
Lấy (1)+(2)
2AH+BC>AB+AC
Đúng 0
Bình luận (0)



