cho g là trọng tâm của tam giác đều abc chứng minh rằng gb=gc =ga
CN
Những câu hỏi liên quan
Cho G là trọng tâm của tam giác đều ABC. Chứng minh rằng:
GA = GB = GC
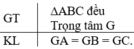
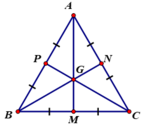
Gọi trung điểm BC, CA, AB lần lượt là M, N, P.
Khi đó AM, BN, CP đồng quy tại trọng tâm G.
Ta có: ∆ABC đều suy ra:
+ ∆ABC cân tại A ⇒ BN = CP (theo chứng minh bài 26).
+ ∆ABC cân tại B ⇒ AM = CP (theo chứng minh bài 26).
⇒ AM = BN = CP (1)
Vì G là trọng tâm của ∆ABC nên theo tính chất đường trung tuyến:
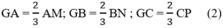
Từ (1) , (2) ⇒ GA = GB = GC.
Đúng 2
Bình luận (0)
Cho G là trọng tâm của tam giác đều ABC. Chứng minh rằng : GA = GB = GC
vì G là trọng tâm của tam giác ABC ta có :
AG=2/3 AN
BG=2/3 BQ (1)
CG=2/3 CM (2)
mà 2 tam giác ACM=ABQ ( g-c-g)
suy ra CM=BQ (cạnh tương ứng) (3)
từ (2) và (3) suy ra BG=CG
>>>>>>.........''tớ chỉ pk lmf tới đây thui''.........<<<<<<<<<<
Đúng 0
Bình luận (0)
cho minh xin vai ******* nha minh can gap lam
Đúng 0
Bình luận (0)
típ theo là :...........
mà AN,CM,BQ là 3 đường trung tuyến của tam giác đều nên :
suy ra : AN=CM=BQ
suy ra: AG=BG=CG
........ko pk đúng sai âu nha..........
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho G là trọng tâm của tam giác đều ABC . Chứng minh rằng:
GA=GB=GC
làm sao để c/m 3 cạnh đó bằng nhau??????????? mk cx ko bít bn giống mk hihi
4536476598769
Đúng 0
Bình luận (0)
Cho G là trọng tâm của tam giác ABC, chứng minh rằng
a) Nếu ABC là tam giác đều thì GA=GB=GC
b) Nếu GA=GB=GC thì ABC là tam giác đều
k cho mình nhe
xét hai tam giác DGB=GEC(c.g.c)
=>BD=EC
mà BD=1/2AB
EC=1/2AC
=>AB=AC
tự Cm tiếp nhe
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho tứ diện ABCD. Gọi G là trọng tâm của tam giác ABC. Chứng minh rằng:
G
D
→
.
G
A
→
+
G
D
→
.
G
B
→
+
G
D...
Đọc tiếp
Cho tứ diện ABCD. Gọi G là trọng tâm của tam giác ABC. Chứng minh rằng: G D → . G A → + G D → . G B → + G D → . G C → = 0
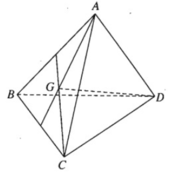
Ta có:
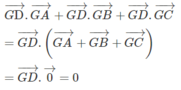
(Vì G là trọng tâm của tam giác ABCD nên 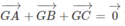 )
)
Đúng 0
Bình luận (0)
Tam giác ABC đều cạnh là 8cm. G là trọng tâm của tam giác ABC, trung tuyến AD, BE, CF.
a/ Tính AD, CG
b/ Chứng minh GA = GB + GC
a: AD=BE=CF=8*căn 3/2=4*căn 3(cm)
CG=2/3*4*căn 3=8/3*căn 3(cm)
b: Vì ΔABC đều có G là trọng tâm
nên G là tâm đường tròn ngoại tiếp
=>GA=GB=GC
Đúng 0
Bình luận (0)
cho G là trọng tâm tam giác đều ABC c/minh GA=GB=GC
đều cạnh là 8cm. G là trọng tâm của tam giác ABC, trung tuyến AD, BE, CF.
a/ Tính AD, CG
b/ Chứng minh GA = GB + GC
Cho tam giác ABC đều, trọng tâm G.
a) Chứng minh GA = GB = GC.
b) Trên tia AG lấy điểm D sao cho G là trung điểm của AD. Chứng minh △BGD đều.



