Hình chữ nhật ABCD có AB = 2BC. Trên cạnh AB lấy một điểm E sao cho DE=DC. Khi đó góc DEC bằng:
Có một miếng bìa hình chữ nhật ABCD với AB=3 và AD=6. Trên cạnh AD lấy điểm E sao cho AE=2, trên cạnh BC lấy điểm F là trung điểm BC
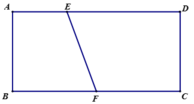
Cuốn miếng bìa lại sao cho cạnh AB và DC trùng nhau để tạo thành mặt xung quanh của một hình trụ. Khi đó tính thể tích V của tứ diện ABEF.
![]()

Hình chữ nhật ABCD có AB = 2BC. Trên cạnh CD lấy một điểm E sao cho EB=AB. Số đo góc DAE bằng
a)Vì tứ giác ABCD là HBH ⇒ AB//CD hay AE//DF
và AD//BC
Xét tứ giác AEFD có AE//DF và AD//EF ⇒tứ giác AEFD là HBH
⇒ AE=DF và AD=EF
Xét ΔADF và ΔFEA có :
DF=AE(chứng minh trên)
AD=EF(chứng minh trên)
AF là cạnh chung
⇒ΔADF=ΔFEA (c.c.c)⇒góc AEF=góc ADF ; góc DAE=góc DFE
b)Xét tứ giác EBCF có EB//FC( vì AB//CD)
EF//BC(gt)
⇒tứ giác EBCF là BHB⇒FC=EB; EF=BC(t/c HBH)
Cho hình chữ nhật ABCD . Có AB bằng 18cm, AD=12cm. Lấy một điểm M trên cạnh BC sao cho MC=MB; lấy một điểm N trên cạnh DC sao cho ND=NC. Tính diện tích hình tam giác AMN
Diện tích hình chữ nhật ABCD là: 12 x 18 = 216 (cm2)
Diện tích tam giác ABM là: (18 x 12:2):2 = 54 (cm2)
Diện tích tam giác ADN là: (12 x18:2):2 = 54 (cm2)
Diện tích tam giác MCN là: (12:2)x(18:2) : 2 = 27 (cm2)
Diện tích tam giác AMN là: 216 - (54+54+27) = 81 (cm2)
Cho hình chữ nhật ABCD . Lấy điểm E trên cạnh AB và biết góc DEC = 90 độ , ED = 3 cm,EC = 4 cm . Tính cạnh AD ?
bài này trong giải toán trên mạng 8 phải ko hả bạn
cho hình chữ nhật abcd có AB=20cm, BC =15 cm. Trên cạnh AB lấy điểm E, trên cạnh BC lấy G sao cho AE = CG = x (cm). Trên cạnh AB lấy diểm F, trên cạnh dc lấy điểm H sao cho AF =CH=2x (cm). Tìm giá trị x để diện tích tứ giác EFGH lớn nhất và tìm giá trị lớn nhất đó.
S_EFGH = S_ABCD - S_BGF - S_GCH - S_AEHD
Là các hình tam giác vuông và hình thang vuông, dễ dàng tìm được hàm diện tích của EFGH theo x: -2x2 + 32.5x
Nếu được thì đạo hàm là tìm được giá trị x mà S max.
cho hình chữ nhật ABCD có AB=8cm, AD=6cm. Gọi M là giao điểm của AC và BD. Trên cạnh DC lấy điểm E sao cho ME vuông góc với BD. Tính độ dài ME
ΔADC vuông tại D
=>\(AC^2=AD^2+DC^2\)
=>\(AC^2=8^2+6^2=100\)
=>AC=10(cm)
ABCD là hình chữ nhật
=>AC cắt BD tại trung điểm của mỗi đường và AC=BD
=>M là trung điểm chung của AC và BD và AC=BD
=>MD=MB=MA=MC=AC/2=5(cm)
Xét ΔDME vuông tại M và ΔDCB vuông tại C có
\(\widehat{MDE}\) chung
Do đó: ΔDME đồng dạng với ΔDCB
=>\(\dfrac{ME}{CB}=\dfrac{DM}{DC}\)
=>\(\dfrac{ME}{6}=\dfrac{5}{8}\)
=>\(ME=3,75\left(cm\right)\)
Cho hình chữ nhật ABCD và điểm E trên cạnh AB
Hãy vẽ đường thẳng đi qua điểm E và vuông góc với cạnh DC, cắt cạnh DC tại điểm G. Ta thu được các hình tứ giác đều là hình chữ nhật, nêu tên các hình chữ nhất đó.
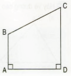
- Các hình chữ nhật là : ABCD, AEGD, EBCG
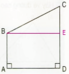
Cho hình chữ nhật ABCD và điểm E trên cạnh AB
Hãy vẽ đường thẳng đi qua điểm E và vuông góc với cạnh DC, cắt cạnh DC tại điểm G. Ta thu được các hình tứ giác đều là hình chữ nhật, nêu tên các hình chữ nhất đó.
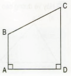
Các hình chữ nhật là : ABCD, AEGD, EBCG
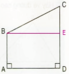
cho hình vuông ABCD . Trên AD lấy điểm F .Trên cạnh DC lấy điểm E . Trên AB lấy điểm G sao cho AF=DE=AG . Gọi I là giao điểm của AE và BF . cmr IG vuông góc với IC