Cho ∆ PQR = ∆DEF trong đó PQ = 8cm, QR = 5cm, PR= 9cm. Chu vi tam giác DEF là
Cho △PQR=△DEF trong đó PQ=5cm,QR=4cm,PR=3cm.
Chu vi tam giác DEF là:
Chu vi của tam giác PRQ là:
5+4+3=12(cm)
Mà theo đề bài thì tam giác PRQ=tam giác DEF
=>chu vi của tam giác DEF là 12cm
Tìm tam giác vuông trong các tam giác sau:
a) Tam giác \(EFK\) có \(EF = 9\)m, \(FK = 12\)m, \(EK = 15\)m.
b) Tam giác \(PQR\) có \(PQ = 17\)cm, \(QR = 12\)cm, \(PR = 10\)cm.
c) Tam giác \(DEF\) có \(DE = 8\)m, \(DF = 6\)m, \(EF = 10\)m.
a: EK^2=EF^2+FK^2
=>ΔEFK vuông tại F
b: PQ^2<>QR^2+PR^2
=>ΔPRQ ko vuông
c: EF^2=DE^2+DF^2
=>ΔDEF vuông tại D
Câu 2: Cho tam giác PQR vuông tại P có PQ = 8cm; PR = 6cm, M là trung điểm của QR. a) Tính QR, PM. b) Từ M vẽ MK, MN lần lượt vuông góc với PR và PQ (K thuộc PQ, N thuộc PR). Tứ giác PNMK là hình gì? Vì sao? c) Gọi O là trung điểm của KM, H là điểm đối xứng của M qua K. Chứng minh: OQ = ON và tứ giác PMQH là hình thoi.
Sửa đề: MK\(\perp\)PQ; MN\(\perp\)PR
a: ta có: ΔPQR vuông tại P
=>\(QR^2=PQ^2+PR^2\)
=>\(QR^2=8^2+6^2=100\)
=>\(QR=\sqrt{100}=10\left(cm\right)\)
Ta có: ΔRPQ vuông tại P
mà PM là đường trung tuyến
nên \(PM=\dfrac{RQ}{2}=5\left(cm\right)\)
b: Xét tứ giác PNMK có
\(\widehat{PNM}=\widehat{PKM}=\widehat{NPK}=90^0\)
=>PNMK là hình chữ nhật
c: Xét ΔRPQ có
M là trung điểm của RQ
MK//RP
Do đó: K là trung điểm của PQ
=>PK=KQ(1)
Ta có: PKMN là hình chữ nhật
=>PK=MN(2)
Từ (1) và (2) suy ra KQ=MN
Ta có: PK//MN
K\(\in\)PQ
Do đó: NM//KQ
Xét tứ giác KQMN có
KQ//MN
KQ=MN
Do đó: KQMN là hình bình hành
=>QN cắt MK tại trung điểm của mỗi đường
mà O là trung điểm của MK
nên O là trung điểm của QN
=>OQ=ON
Xét tứ giác PMQH có
K là trung điểm chung của PQ và MN
=>PMQH là hình bình hành
Hình bình hành PMQH có PQ\(\perp\)MH
nên PMQH là hình thoi
giải tam giác PQR vuông tạp P biết PQ =5cm PR = 8cm
Cho tam giác PQR nhọn PQ < PR lấy M thuộc cạnh PQ, N thuộc cạnh PR sao cho MN//QR
cho biết PQ=8cm MQ=6cm NP=3cm
p/s EM ĐANG GẤP NHA MN
Vẽ tam giác PQR có PQ=PR=5cm, QR=6cm.
Lấy M trên QR sao cho PM=4,5cm. có bao nhiêu M như vậy?
M có nằm trên cạnh QR không? Tại sao?
Ta có Tam giác PQR cân tại P vì PQ=PR
Kẻ đường cao PH của Tam giác PQR ta có
Vì Tam giác PQR cân tại P => H là trung điểm RQ => HR=HQ=1/2.RQ=1/2.6=3(cm)
Tam giác PRH vuông tại H, Áp dụng ĐL Pytago có
\(PR^2=RH^2+PH^2\)
\(5^2=3^2+PH^2\)=> PH=4cm
Xét Tam giác PMH vuông tại H, áp dụng PYtago ta có
\(PM^2=PH^2+MH^2\)
\(4.5^2=4^2+MH^2\)
=> MH=\(\sqrt{4.5^2-4^2}\)
Nếu M thuộc đoạn RH (TM)
Nếu M thuộc đoạn QH (TM)
Vậy có 2 đuiểm M thảo mãn yêu cầu
(P/s) có thể Ah trình bày ko đúng lém đâu hen
_Kudo_
câu 1.cho tam giác ABC vuông tại B.Biết AC =căn bậc 34 cm ,BC=3cm. khi dó độ dài AB là
A.5cm B.căn bậc 34 C.căn bậc 37 D.4cm
câu 2.cho tam giác PQR có PQ=PR=2cm,QR= căn bậc 8.Ta có tam giác PQR là
A.tam giác cân tại P B.tam giác vuông tại P C.tam giác vuông tại Q D.tam giác vuông cân tại P
Đố: Vẽ tam giác PQR có PQ = PR = 5cm, QR = 6 cm.
Lấy điểm M trên đường thẳng QR sao cho PM = 4,5cm. Có mấy điểm M như vậy?
Điểm M có nằm trên cạnh QR hay không? Tại sao?
* Vẽ hình:
- Vẽ tam giác PQR có PQ = PR = 5cm, QR = 6cm.
+ Vẽ đoạn thẳng QR = 6cm.
+ Vẽ cung tròn tâm Q và cung tròn tâm R bán kính 5cm. Hai cung tròn này cắt nhau tại P.
+ Nối PQ và PR ta được tam giác cần vẽ.
- Vẽ điểm M : Vẽ cung tròn tâm P bán kính 4,5cm cắt QR (nếu có) tại M.
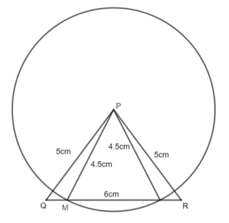
Vậy ta có thể vẽ được 2 điểm M trên đường thẳng QR để PM = 4.5cm
* Kẻ đường cao PH của ΔPQR
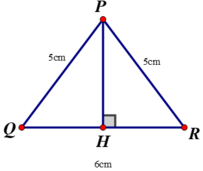
Xét hai tam giác vuông tại H: ΔPHQ và ΔPHR có
PH chung
PQ = PR ( = 5cm)
⇒ ΔPHQ = ΔPHR (cạnh huyền – cạnh góc vuông)
⇒ HQ = HR (Hai cạnh tương ứng)
Mà HQ + HR = QR = 6 cm
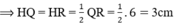
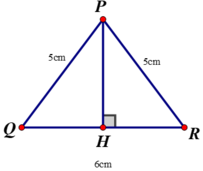
+ ΔPHR vuông tại H có PR2= PH2+ HR2(định lí Py – ta – go)
⇒ PH2= PR2– HR2= 52– 32= 16 ⇒ PH = 4cm .
Đường vuông góc PH = 4cm là đường ngắn nhất trong các đường kẻ P đến đường thẳng QR.
Vậy chắc chắn có đường xiên PM = 4,5cm (vì PM = 4,5cm > 4cm) kẻ từ P đến đường thẳng QR.
+ Lại có : HM, HR lần lượt là hình chiếu của các đường xiên PM, PR trên đường thẳng QR.
Mà PM < PR ⇒ HM < HR = HQ (đường xiên nào lớn hơn thì hình chiếu lớn hơn).
⇒ M nằm giữa H và Q hoặc H và R
⇒ M nằm trên cạnh QP và có hai điểm M như vậy.
Cho ∆ PQR vuông tại P và ∆ DEF vuông ởD có PQ = DE, cần có thêm điềukiện gì để∆ PQR = ∆ DEF theo trường hợp cạnh-góc-cạnh :
A.PR = DF
B.Q^=E^̂̂
C. QR = EF
D.R^=F^̂̂