Tìm x
1/2x3x+1/3x4x+1/4x5x+...+1/49x50
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
MC
Những câu hỏi liên quan
3x+1+3x+2-2x3x=270 tìm x
3x+1 + 3x+2 - 2 x 3x = 270
3x ( 3 + 32 - 2) = 270
3x . 10 = 270
3x = 270 : 10
3x = 27
3x = 33
x = 3
Đúng 2
Bình luận (0)
\(3^{x+1}+3^{x+2}-2.3^x=270\)
\(\Leftrightarrow3.3^x+3^2.3^x-2.3^x=270\)
\(\Leftrightarrow\left(3+3^2-2\right).3^x=270\)
\(\Leftrightarrow10.3^x=270\)
\(\Leftrightarrow3^x=27\)
\(\Leftrightarrow3^x=3^3\)
\(\Leftrightarrow x=3\)
Đúng 0
Bình luận (0)
Tìm các tiệm cận đường và ngang của đồ thị mỗi hàm số sau: y = 3 - 2 x 3 x + 1
Từ
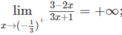
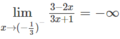
ta có x = −1/3 là tiệm cận đứng
Vì
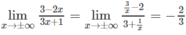
nên đường thẳng y = -2/3 là tiệm cận ngang.
Đúng 0
Bình luận (0)
Tập nghiệm của bất phương trình
x
-
1
2
-
3
x
4
x
+
1
≥
0
là A.
-
∞
;
-...
Đọc tiếp
Tập nghiệm của bất phương trình x - 1 2 - 3 x 4 x + 1 ≥ 0 là
A. - ∞ ; - 1 4 ∪ 2 3 ; 1
B. - ∞ ; - 1 4 ∪ 2 3 ; 1
C. ( - 1 4 ; 2 3 ] ∪ [ 1 ; + ∞ )
D. ( - ∞ ; - 1 4 ) ∪ [ 1 ; + ∞ )
Giá trị nhỏ nhất của hàm số
x
-
1
2
-
3
x
4
x
+
1
≥
0
là A. 3 B. 13 C. 16 D. 19
Đọc tiếp
Giá trị nhỏ nhất của hàm số x - 1 2 - 3 x 4 x + 1 ≥ 0 là
A. 3
B. 13
C. 16
D. 19
Thực hiện phép tính sau
(
2
x
3
x
+
1
−
1
)
:
(
1
−
8
x
2
9
x
2
−
1
)
, ta được kế...
Đọc tiếp
Thực hiện phép tính sau ( 2 x 3 x + 1 − 1 ) : ( 1 − 8 x 2 9 x 2 − 1 ) , ta được kết quả là
A. 1 − 3 x x − 1
B. 3 x − 1 x − 1
C. − ( 3 x + 1 ) x − 1
D. 1 − 3 x − x − 1
Thực hiện phép tính sau
(
2
x
3
x
+
1
−
1
)
:
(
1
−
8
x
2
9
x
2
−
1
)
, ta được kết quả là: A.
1
−...
Đọc tiếp
Thực hiện phép tính sau ( 2 x 3 x + 1 − 1 ) : ( 1 − 8 x 2 9 x 2 − 1 ) , ta được kết quả là:
A. 1 − 3 x x − 1
B. 3 x − 1 x − 1
C. − ( 3 x + 1 ) x − 1
D. 1 − 3 x − x − 1
3
x
1
-
3
x
+
2
x
3
x
+
1
:
6
x
2
+
10
x
1...
Đọc tiếp
3 x 1 - 3 x + 2 x 3 x + 1 : 6 x 2 + 10 x 1 - 6 x + 9 x 2
1/1x2 + 1/2x3 +...+ 1/49x50 = ?
\(\frac{1}{1.2}+\frac{1}{2.3}+...+\frac{1}{49.50}=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+...+\frac{1}{49}-\frac{1}{50}=\frac{49}{50}\)
Đúng 0
Bình luận (0)
\(\frac{1}{1.2}+\frac{1}{2.3}...\frac{1}{49.50}\)
\(=\frac{1}{1}-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+...\frac{1}{49}-\frac{1}{50}\)
\(=\frac{1}{1}-\frac{1}{50}\)
\(=\frac{49}{50}\)
Đúng 0
Bình luận (0)
a = 1\1x2+1\2x3+1\3x4+........+1\49x50
Ta có công thức \(\frac{a}{b.c}=\frac{a}{c-b}.\left(\frac{1}{b}-\frac{1}{c}\right)\)
Dựa vào công thức trên, ta có
\(\frac{1}{1.2}=\frac{1}{2-1}.\left(1-\frac{1}{2}\right)\)
\(\frac{1}{2.3}=\frac{1}{3-2}.\left(\frac{1}{2}-\frac{1}{3}\right)\)
............................................
\(\frac{1}{49.50}=\frac{1}{50-49}.\left(\frac{1}{49}-\frac{1}{50}\right)\)
\(A=1.\left(1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+....+\frac{1}{49}-\frac{1}{50}\right)\)
\(\Rightarrow A=1-\frac{1}{50}=\frac{49}{50}\)
chắc chắn bạn ạ, ai thấy đúng hì ủng hộ nha
Đúng 0
Bình luận (0)
\(A=\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+...+\frac{1}{49.50}=1-\frac{1}{50}=\frac{49}{50}\)\(\frac{49}{50}\)
Đúng 0
Bình luận (0)
A = \(\frac{1}{1\times2}+\frac{1}{2\times3}+...+\frac{1}{49\times50}\)
A = \(\frac{1}{1}-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+...+\frac{1}{49}-\frac{1}{50}\)
A = \(\frac{1}{1}-\frac{1}{50}\)
A = \(\frac{50}{50}-\frac{1}{50}\)
A = \(\frac{49}{50}\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời