Cho tam giác ABC có .
Các đường trung trực của AB và AC cắt nhau tại I.
Khi đó
DV
Những câu hỏi liên quan
Cho tam giác ABC có .
Các đường trung trực của AB và AC cắt nhau tại I.
Khi đó góc BIC=
Cho tam giác ABC, đường trung trực của AB và AC cắt nhau tại E. Khi đó
A. EA < EB < EC
B. EA = EB = EC
C. EA < EB = EC
D. EA = EB < EC
Cho tam giác ABC, đường trung trực của AB và AC cắt nhau tại E. Khi đó
A. EA < EB < EC
B. EA = EB = EC
C. EA < EB = EC
D. EA = EB < EC
Cho tam giác ABC cân tại A, M là trung điểm BC. Đường trung trực của AB và AC cắt nhau tại D. Khi đó ta có:
A. Ba điểm A, D, M thẳng hàng
B. Ba điểm A, D, C thẳng hàng
C. Ba điểm A, D, B thẳng hàng
D. Ba điểm B, D, C thẳng hàng
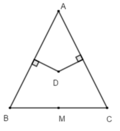
D là giao điểm của hai đường trực của hai cạnh AB và AC nên D là giao của ba đường trung trực trong tam giác ABC
Suy ra D thuộc đường trung trực của đoạn thẳng BC (1)
Lại có M là trung điểm của BC nên AM là trung tuyến của tam giác ABC cân tại A
Do đó AM là đường trung trực của BC (trong tam giác cân, trung tuyến tại đỉnh đồng thời cũng là đường trung trực ứng với đáy) (2)
Từ (1) và (2) suy ra A, D, M thẳng hàng nên A đúng.
Do tam giác ABC cân nên giao điểm D của ba đường trung trực của tam giác ABC không thuộc các đường thẳng AB, AC, BC nên B, C, D sai.
Chọn đáp án A
Đúng 0
Bình luận (0)
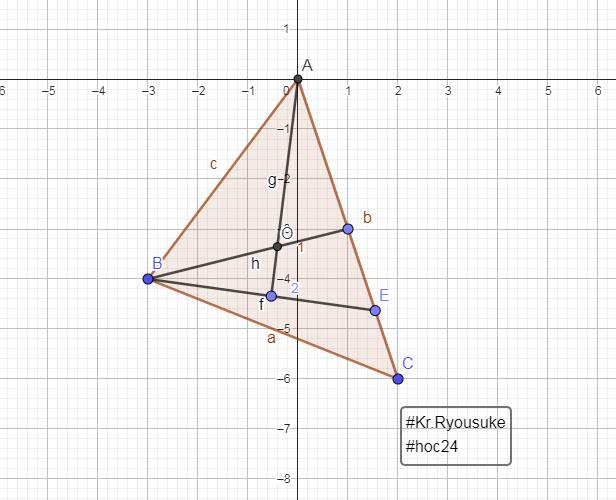
Cho Tam giác ABC có AC>AB. Trên cạnh AC lấy điểm E sao cho CE=AB. Các đường trung trực của BE và AC cắt nhau tại O. Khi đó
A. AO là tia phân giác của góc A
B. AO vuông góc với BC
C. Ao là đươfng trung tuyến của Tam giác ABC
D.Ao là đường trunng trực của tam giác ABC
Vì các đường trung trực của `\Delta ABC` cắt nhau tại điểm O
`->` `\text {AO}` là đường trung trực thứ `3` của `\Delta`
Xét các đáp án trên `-> D.`
Đúng 0
Bình luận (0)
Cho Tam giác ABC có góc A= 40 độ. Các đường trung trực của AB và AC cắt nhau tại I . Khi đó góc BIC = ? độ
Ghi cách giải cho mình với . Cảm ơn nhiều
Xem thêm câu trả lời
Cho tam giác ABC có ∠A = 130o. Gọi C', B'là các điểm sao cho AB là đường trung trực của CC' và AC là đường trung trực của BB'. Hai đường thẳng CB' và BC' cắt nhau tại A'. Hãy tìm bên trong tam giác A'BC điểm cách đều ba cạnh của tam giác đó.
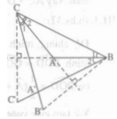
+) Vì AC là đường trung trực của BB'
Suy ra: CB’ =CB ( tính chất đường trung trực)
Do đó,tam giác CBB’ là tam giác cân tại C. Có CA là đường trung trực của BB’ nên đồng thời là đường phân giác nên có ∠C1= ∠C2.
+) Vì AB là đường trung trực của CC' nên BC = BC’.
Suy ra, tam giác BCC’ cân tại B. Lại có BA là đường trung trực nên đồng thời là đường phân giác (tính chất tam giác cân).
Suy ra: ∠B1 = ∠B2 .
+) Ta có: AB, AC lần lượt là đường phân giác của các góc A'BC và góc A'CB; hai đường này cắt nhau tại A.
Vậy ba đường phân giác của tam giác A'BC đồng quy tại A, hay A là điểm nằm trong tam giác A'BC và cách đều ba cạnh của tam giác này.
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại , các đường trung trực của AB và AC cắt nhau tại O và cắt BC tại D và E. CMR:
a) OA là đường trung trực của BC
b) BD = CE
c) Tam giác ODE cân
giúp mình nhanh với , với vẽ hình cho mình luôn nha cảm ơn trước
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại , các đường trung trực của AB và AC cắt nhau tại O và cắt BC tại D và E. CMR:
a) OA là đường trung trực của BC
b) BD = CE
c) Tam giác ODE cân
trả lời nhanh cho mình nha mình cảm ơn trước
Đúng 1
Bình luận (0)
Câu 1 :Cho tam giác ABC có góc B-góc C 40 độ Đường trung trực của BC cắt AC ở I Tính số đo góc ABICâu 2 :Tam giác ABC có AB6 BC4 Qua trung điểm M của AC kẻ đường thẳng vuông góc với AC cắt A tại I Tính chu vi tam giác IBC Câu 3 :Cho góc xOy 60 độ điểm A nằm trong góc đó Vẽ các điểm B và C sao cho Ox là đường trung trực của AB. Oy là đường trung trực của AC Tính các góc của tam giác OBC
Đọc tiếp
Câu 1 :Cho tam giác ABC có góc B-góc C =40 độ Đường trung trực của BC cắt AC ở I Tính số đo góc ABI
Câu 2 :Tam giác ABC có AB=6 BC=4 Qua trung điểm M của AC kẻ đường thẳng vuông góc với AC cắt A tại I Tính chu vi tam giác IBC Câu 3 :Cho góc xOy = 60 độ điểm A nằm trong góc đó Vẽ các điểm B và C sao cho Ox là đường trung trực của AB. Oy là đường trung trực của AC Tính các góc của tam giác OBC
Câu 1.
Gọi DI là trung trực BC
Xét ΔBIDvà ΔCID:
IDchung
\(\widehat{BDI}=\widehat{CDI}=90^o\)(ID trung trực BC)
BD = CD(như trên)
⇒ΔBID = ΔCID (c.g.c )
⇒ \(\widehat{IBD}=\widehat{C}\)(2gtu)
\(\widehat{B}-\widehat{C}\) = 40
hay \(\widehat{B}-\widehat{IBD}\) = 40
Mà\(\widehat{IBD}+\widehat{ABI}=B\)
\(\Rightarrow\widehat{ABI}=\widehat{B}-\widehat{IBD}=40^o\)


