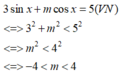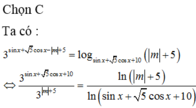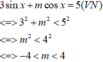Tìm tất cả các giá trị của tham số thực m để phương trình 3sinx - 5cosx = m vô nghiệm.
NL
Những câu hỏi liên quan
Tìm tất cả các giá trị của tham số thực m để phương trình
3
sin
x
+
m
cos
x
5
vô nghiệm. A.
m
4
B.
m
−
4
C.
m
≥
4
D.
−
4
m
4
Đọc tiếp
Tìm tất cả các giá trị của tham số thực m để phương trình 3 sin x + m cos x = 5 vô nghiệm.
A. m > 4
B. m < − 4
C. m ≥ 4
D. − 4 < m < 4
Tìm tất cả các giá trị thực của tham số m để phương trình
y
5
cos
x
−
m
sin
x
m
+
1
có nghiệm A.
m
≤
12
B.
m
≤
−
13
C.
m
≤
24
D.
m
≥
24
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để phương trình y = 5 cos x − m sin x = m + 1 có nghiệm
A. m ≤ 12
B. m ≤ − 13
C. m ≤ 24
D. m ≥ 24
Tìm các giá trị m để phương trình
3
sin
x
+
5
cos
x
-
m
+
5
log
sin
x
+
5
cos
x...
Đọc tiếp
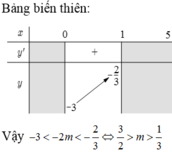
Tìm các giá trị m để phương trình 3 sin x + 5 cos x - m + 5 = log sin x + 5 cos x + 10 m + 5 có nghiệm
![]()
![]()
![]()
![]()
Cho phương trình
m
+
1
2
x
+
1
7
m
-
5
x
+
m
. Tìm tất cả các giá trị thực của tham số m để phương trình đã cho vô nghiệm. A. m 1. B. m 2; m 3. C. m 2. D. m 3.
Đọc tiếp
Cho phương trình m + 1 2 x + 1 = 7 m - 5 x + m . Tìm tất cả các giá trị thực của tham số m để phương trình đã cho vô nghiệm.
A. m = 1.
B. m = 2; m = 3.
C. m = 2.
D. m = 3.
Phương trình viết lại m 2 − 5 m + 6 x = m − 1
Phương trình vô nghiệm khi m 2 − 5 m + 6 = 0 m − 1 ≠ 0 ⇔ m = 2 m = 3 m ≠ ⇔ m = 2 m = 3
Đáp án cần chọn là: B
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị của tham số thực m để phương trình 3 . sin x + m . cos x = 0 vô nghiệm.
A. m > 4
B. m < -4
C. - 4 < m < 4
D. tất cả đều sai
Tìm tất cả các giá trị của tham số m để phương trình:
1
3
cos
3
x
-
3
cos
2
x
+
5
cos
x
-
3
+
2
m
0
có đúng bốn nghiệm thuộc đoạn
0
;...
Đọc tiếp
Tìm tất cả các giá trị của tham số m để phương trình: 1 3 cos 3 x - 3 cos 2 x + 5 cos x - 3 + 2 m = 0 có đúng bốn nghiệm thuộc đoạn 0 ; 2 π
A. - 3 2 < m < - 1 3
B. 1 3 ≤ m < 3 2
C. 1 3 < m < 3 2
D. - 3 2 ≤ m < - 1 3
Tìm tất cả các giá trị thực của tham số m để phương trình
log
2
cos
x
-
m
log
cos
2
x
-
m
2
+
4
0
vô nghiệm A.
m
∈
2
;
2
B. ...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để phương trình log 2 cos x - m log cos 2 x - m 2 + 4 = 0 vô nghiệm
A. m ∈ 2 ; 2
B. m ∈ - 2 ; 2
C. m ∈ - 2 ; 2
D. - 2 ; 2
Điều kiện:
cos x # 0 ⇔ x # π 2 + k π , k ∈ ℝ .
Ta có:
![]()
![]()
Đặt t=log|cosx|. Do 0 < | cos x | ≤ 1 nên log cos x ≤ 0 hay t ∈ ( - ∞ ; 0 ]
Phương trình trở thành t 2 - 2 m t - m 2 + 4 = 0 *
có ∆ ' = m 2 + m 2 - 4 = 2 m 2 - 4
Phương trình đã cho vô nghiệm nếu và chỉ nếu phương trình (*) vô nghiệm hoặc có 2 nghiệm (không nhất thiết phân biệt) t 1 , t 2 thỏa mãn 0 < t 1 ≤ t 2
TH1: (*) vô nghiệm ![]()
TH2: (*) có hai nghiệm thỏa mãn 0 < t 1 ≤ t 2
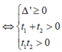
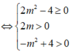
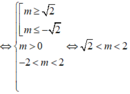
Kết hợp hai trường hợp ta được m ∈ - 2 ; 2
Chọn đáp án C.
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị thực của tham số m để phương trình (m^2-4)x=3m+6 vô nghiệm
cần gấp
\(\left(m^2-4\right)x=3m+6\Leftrightarrow\left(m^2-4\right)x-3m-6=0\) vô nghiệm
\(\Leftrightarrow\left\{{}\begin{matrix}m^2-4=0\\-3m-6\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}m=2\\m=-2\end{matrix}\right.\\m\ne-2\end{matrix}\right.\Leftrightarrow m=2\)
Đúng 3
Bình luận (3)
Tìm tất cả các giá trị thực của tham số m để phương trình
log
2
cos
x
-
m
log
cos
2
x
-
m
2
+4 0 vô nghiệm.
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để phương trình log 2 cos x - m log cos 2 x - m 2 +4 = 0
vô nghiệm.
![]()
![]()
![]()
![]()
Chọn C.
Phương pháp:
- Đặt t = log cos x và tìm điều kiện của t .
- Thay vào phương trình đã cho đưa về phương trình ẩn t .
- Biến đổi điều kiện bài toán về điều kiện của phương trình vừa có được và tìm m .
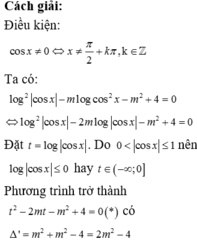

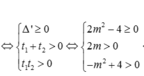
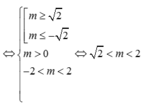
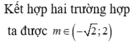
Đúng 0
Bình luận (0)