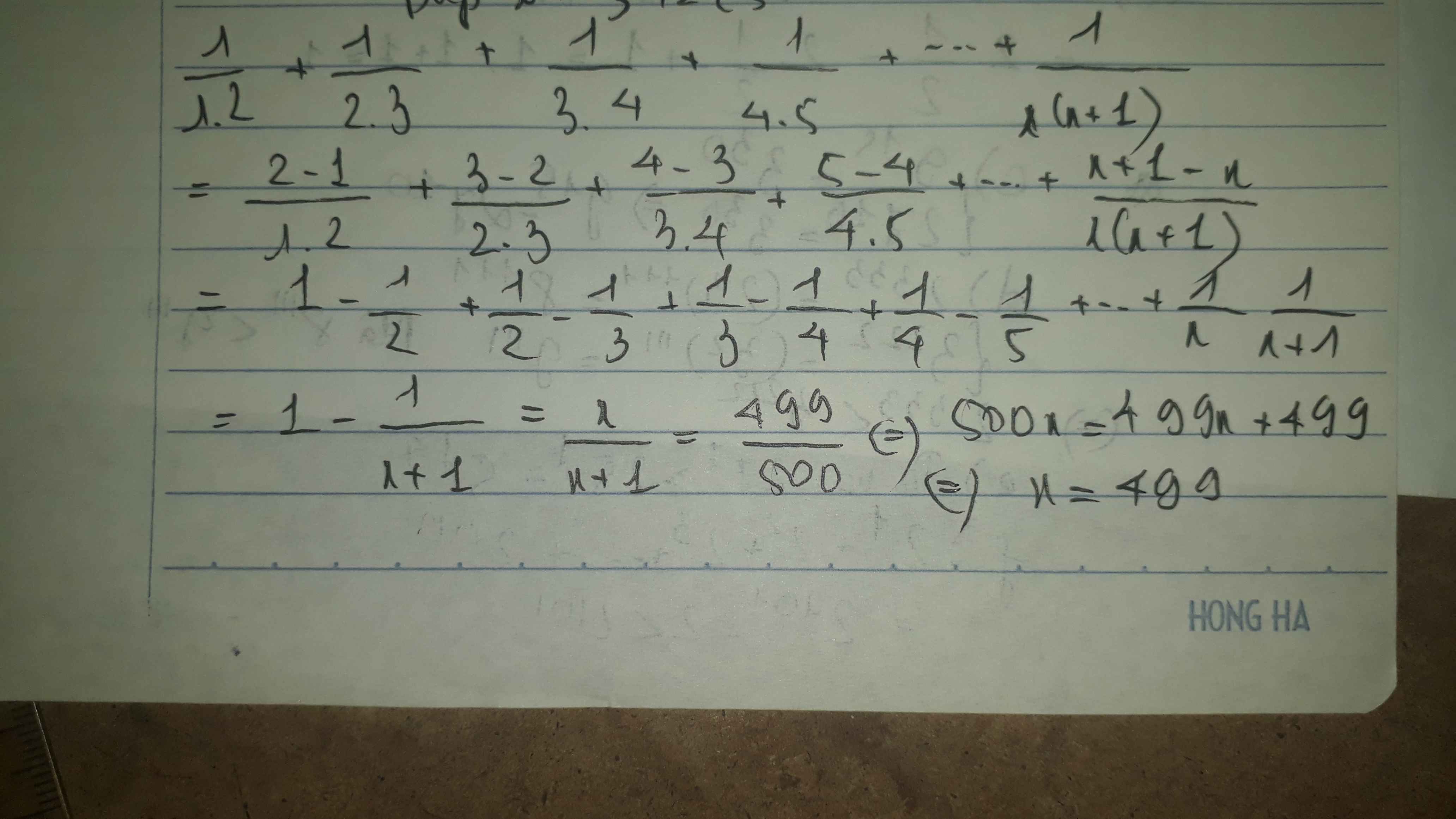ta có:

1-1/2+1/2-1/3+1/3-1/4+....+1/x -1/x+1 =499/500

1-1/x+1 =499/500

1/x+1 =1/500 

x+1=500

x=499

\(\frac{1}{1\times2}+\frac{1}{2\times3}+\frac{1}{3\times4}+...+\frac{1}{X\times\left(X+1\right)}=\frac{499}{500}\)

\(\Leftrightarrow1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{X}-\frac{1}{X+1}=\frac{499}{500}\)

\(\Leftrightarrow1-\frac{1}{X+1}=\frac{499}{500}\)

\(\Leftrightarrow\frac{1}{X+1}=\frac{1}{500}\)

\(\Leftrightarrow X+1=500\)

\(\Leftrightarrow X=499\)

1x2 là mẫu à?

\(\dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+\dfrac{1}{4.5}+...+\dfrac{1}{x.\left(x+1\right)}=\dfrac{499}{500}\)

\(\Leftrightarrow1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{x}-\dfrac{1}{x+1}=\dfrac{499}{500}\)

\(\Leftrightarrow1-\dfrac{1}{x+1}=\dfrac{499}{500}\)

\(\Leftrightarrow x=499\)

giúp e vs

\(\frac{1}{1}-\frac{1}{2}+\frac{1}{2}-....-\frac{1}{x+1}=\frac{499}{500}\)

1 - 499/500 = 1/x + 1

1/500 = 1/x+1

x + 1 = 500

x = 499

a) 1/1.2 + 1/2.3 + 1/3.4 + .... + 1/x.(x+1) = 499/500

1 - 1/2 + 1/2 - 1/3 + 1/3 - 1/4 + .... + 1/x - 1/x+1 = 499/500

1 - 1/x+1 = 499/500

1/x+1 = 1 - 499/500

1/x+1 = 1/500

x + 1 = 500

     x = 500 - 1 

     x = 499

b) 1/1.3 + 1/3.5 + 1/5.7 + .... + 1/x.(x+2) = 20/41

1/2 . [ 2/1.3 + 2/3.5 + 2/5.7 + ... + 2/x.(x+2) ] = 20/41

1/2 . [ 1 - 1/3 + 1/3 - 1/5 + 1/5 - 1/7 + ... + 1/x - 1/x+2 ] = 20/41

1/2 . [ 1 - 1/x+2 ) = 20/41

1 - 1/x+2 = 20/41 : 1/2

1 - 1/x+2 = 40/41

1/x+2 = 1 - 40/41

1/x+2 = 1/41

x + 2 = 41

      x = 41 - 2 

      x = 39

S = 1-1/2 + 1/3-1/4 + 1/5-1/6 + ..... 1/499-1/500 = (1 + 1/3 + 1/5 + ..+ 1/499) - (1/2 + 1/4 + 1/6 + ...+ 1/500) - (1/2 + 1/4 + 1/6 + ...+ 1/500) + (1/2 + 1/4 + 1/6 + ...+ 1/500) S = (1 + 1/2 + 1/3 + 1/4 + ....+ 1/500) - 2.(1/2 + 1/4 + 1/6 + ...+ 1/500) = (1 + 1/2 + 1/3 + 1/4 + ....+ 1/500)- (1 + 1/2 + 1/3 + ...+1/250) = 1/251 + 1/252 + ...+ 1/500.

Vậy S = 1/251 + 1/252 + ...+ 1/500

S = 1-1/2 + 1/3-1/4 + 1/5-1/6 + ..... 1/499-1/500

= (1 + 1/3 + 1/5 + ..+ 1/499) - (1/2 + 1/4 + 1/6 + ...+ 1/500) - (1/2 + 1/4 + 1/6 + ...+ 1/500) + (1/2 + 1/4 + 1/6 + ...+ 1/500)

S = (1 + 1/2 + 1/3 + 1/4 + ....+ 1/500) - 2.(1/2 + 1/4 + 1/6 + ...+ 1/500)

= (1 + 1/2 + 1/3 + 1/4 + ....+ 1/500)- (1 + 1/2 + 1/3 + ...+1/250)

= 1/251 + 1/252 + ...+ 1/500.

Vậy S = 1/251 + 1/252 + ...+ 1/500

a) -287 + 499 + (-499) + 285

=-287+285

=-2

b: Ta có: \(1992+\left(-53\right)+158+\left(-247\right)+\left(-1592\right)\)

\(=\left(1992-1592\right)+\left(-53-247\right)+158\)

\(=400-300+158=258\)