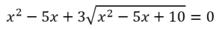5x-10=10
HT
Những câu hỏi liên quan
|x +10| - (5 - 3x) = (4x - 10) - (x - 5)
|3x + 21| - ( 10 - 5x ) = 5x - |-20|
a) | x + 10 | - ( 5 - 3x ) = ( 4x - 10 ) - ( x - 5 )
=> | x + 10 | = ( 5 - 3x ) + ( 4x - 10 ) - ( x - 5 )
=> | x + 10 | = 5 - 3x + 4x - 10 - x + 5
=> | x +10 | = 0
=> x + 10 = 0
=> x = -10
Vậy...
b) Làm tương tự
Kết quả : | 3x + 21 | = -10 ( vô lí) ( vì |3x+21| >= 0 mà -10<0)
Vậy không tìm được x thỏa mãn bài toán
Tìm x biết
|5x-10|+10=5x
| 5x - 10 | + 10 = 5x
<=> | 5x -10 | = 5x -10 . ĐK \(x\ge2\)
\(\Leftrightarrow\orbr{\begin{cases}5x-10=5x-10\\5x-10=10-5x\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}0x=0\\10x=20\end{cases}\Leftrightarrow\orbr{\begin{cases}\text{vô số nghiệm }\\x=2\end{cases}}}\)
Vậy \(S=\left\{x\in R/x\ge2\right\}\)
Đúng 0
Bình luận (0)
Cho biểu thức
P
5
x
+
2
x
-
10
+
5
x
-
2
x
+
10
x
2...
Đọc tiếp
Cho biểu thức P = 5 x + 2 x - 10 + 5 x - 2 x + 10 x 2 - 100 x 2 - 4 . Chứng minh giá trị P = 10 với mọi x ≠ ±10
Điều kiện xác định của phân thức: x ≠ -10, x ≠ 10
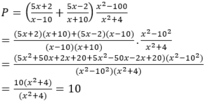
Vậy giá trị P =10 với mọi x ≠ ± 10
Đúng 0
Bình luận (0)
tính ( rút gọn)
(x-10)^2 - 2(x-10)(5x-3)+(5x-3)^2
\(\left(x-10\right)^2-2\left(x-10\right)\left(5x-3\right)+\left(5x-3\right)^2\)
\(=\left(x-10-5x+3\right)^2=\left(-4x-7\right)^2=\left(4x+7\right)^2\)
\(=16x^2+56x+49\)
Đúng 2
Bình luận (0)
Ta có: \(\left(x-10\right)^2-2\left(x-10\right)\left(5x-3\right)+\left(5x-3\right)^2\)
\(=\left(x-10-5x+3\right)^2\)
\(=\left(-4x+6\right)^2\)
\(=16x^2-48x+36\)
Đúng 1
Bình luận (0)
Cho phương trình
x
2
-
5
x
+
3
x
2
-
5
x
+
10
0
. Đặt
t
x
2
-
5
x
+
10
(
t
...
Đọc tiếp
Cho phương trình x 2 - 5 x + 3 x 2 - 5 x + 10 = 0 . Đặt t = x 2 - 5 x + 10 ( t ≥ 0 ) . Khi đó, phương trình đã cho trở thành phương trình
![]()
![]()
![]()
![]()
Giải và biện luận theo m phương trình
| 5x-|5x-10| |=10(m^2)x
Cho \(\sqrt{x^2-5x+14}-\sqrt{x-5x+10}=2\)
Tính \(M=\sqrt{x^2-5x+14}+\sqrt{x^2-5x+10}\)
Đặt \(\sqrt{x^2-5x+14}=a\) và \(\sqrt{x^2-5x+10}=b\) \(\left(a,b>0\right)\)
\(\Rightarrow a-b=2\)
\(\Rightarrow a^2-b^2=x^2-5x+14-x^2+5x-10=4\)
\(\Leftrightarrow\left(a-b\right)\left(a+b\right)=4\)
\(\Leftrightarrow a-b=2\)
\(\Leftrightarrow\sqrt{x^2-5x+14}+\sqrt{x^2-5x+10}=2\left(đpcm\right)\)
Đúng 0
Bình luận (0)
Cho biểu thức \(\sqrt{x^2-5x+14}-\sqrt{x^2-5x+10}=2\). Tính \(A=\sqrt{x^2-5x+14}+\sqrt{x^2-5x+10}\)
ta có
\(2A=\left(\sqrt{x^2-5x+14}-\sqrt{x^2-5x+10}\right)\left(\sqrt{x^2-5x+14}+\sqrt{x^2-5x+10}\right)\)
⇔ 2A=x2-5x+14-x2+5x-10
⇔2A= 4
⇔ A=2
Đúng 0
Bình luận (0)
10-5x(x-1,2)+2x(2,5x-3)=10