cho tam giác abc có ab = ac . gọi I là trung điểm của bc
H24
Những câu hỏi liên quan
Cho tam giác ABC có AB=AC Gọi H là trung điểm của BC a Chứng minh tam giác ABH = tam giác ACH và AB vuông góc vói BC
b gọi E là trung điểm của AC trên tia đối của tia EH . Lấy điểm K Sao cho EK = EH .Chứng minh Ak // BC
c Chứng minh HK = AB
d Gọi I là trung điểm của AH .Chứng minh 3 điểm B I K thẳng hàng
cho tam giác ABC vuông tại A có AB=3cm,BC=5cm. Gọi N là trung điểm BC, trên tia đối N lấy điếm D sao cho ND=NA
a)C/m: tam giác ACN= tam giác DBN
b)Tính BD
c)Gọi M là trung điểm AB. C/m: tam giác MDC cân
d)MD cắt BC tại H, gọi I là trung điểm của AC, DI cắt BC tại K. C/m: tam giác HBD= tam giác KCA
a) Xét ΔACN và ΔDBN có
NA=ND(gt)
\(\widehat{ANC}=\widehat{DNB}\)(hai góc đối đỉnh)
NC=NB(N là trung điểm của BC)
Do đó: ΔACN=ΔDBN(c-g-c)
Đúng 1
Bình luận (0)
b) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(AB^2+AC^2=BC^2\)
\(\Leftrightarrow AC^2=BC^2-AB^2=5^2-3^2=16\)
hay AC=4(cm)
Ta có: ΔACN=ΔDBN(cmt)
nên AC=DB(hai cạnh tương ứng)
mà AC=4cm(cmt)
nên BD=4cm
Vậy: BD=4cm
Đúng 1
Bình luận (0)
c) Xét ΔCAM vuông tại A và ΔDBM vuông tại B có
AC=BD(cmt)
MA=MB(M là trung điểm của AB)
Do đó: ΔCAM=ΔDBM(hai cạnh góc vuông)
Suy ra: MC=MD(Hai cạnh tương ứng)
Xét ΔMCD có MC=MD(cmt)
nên ΔMCD cân tại M(Định nghĩa tam giác cân)
Đúng 0
Bình luận (1)
Cho tam giác ABC có AB = AC, gọi D là trung điểm của BC. Chứng minh: a) Tam giác ADB = ADC; b) AD là tia phân giác của góc BAC; c) AD vuông góc BC
Cho tam giác ABC có AB = AC, gọi D là trung điểm của BC. Chứng minh
a) Tam giác ADB = ADC
b) AD là tia phân giác của góc BAC
c) AD vuông góc BC
Cho tam giác ABC có AB < AC , các đường phân giác AD, BE lần lượt của góc A, góc B cắt nhau tại I. Gọi G là trọng tâm của tam giác ABC ( M là trung điểm của BC ).Có AB= 12cm, AC= 18cm, BC = 15cm.
Chứng minh IG//BC.
Xét ΔABC có AD là phân giác
nên BD/AB=CD/AC
=>BD/2=CD/3=(BD+CD)/(2+3)=15/5=3
=>BD=6cm và CD=9cm
Xét ΔBAD có BI là phân giác
nên AI/ID=AB/BD=2
=>AI/AD=2/3=AG/AM
=>IG//BC
Đúng 0
Bình luận (0)
Cho tam giác ABC có AB < AC , các đường phân giác AD, BE lần lượt của góc A, góc B cắt nhau tại I. Gọi G là trọng tâm của tam giác ABC ( M là trung điểm của BC ).Có AB= 12cm, AC= 18cm, BC = 15cm.
Chứng minh IG//BC.
Xét ΔABC có AD là phân giác
nên BD/AB=CD/AC
=>BD/2=CD/3=(BD+CD)/(2+3)=15/5=3
=>BD=6cm và CD=9cm
Xét ΔBAD có BI là phân giác
nên AI/ID=AB/BD=2
=>AI/AD=2/3=AG/AM
=>IG//BC
Đúng 0
Bình luận (0)
Cho tam giác ABC có AB=AC Gọi H là trung điểm của BC
a Chứng minh tam giác ABH = tam giác ACH và AB vuông góc vói BC
b gọi E là trung điểm của AC trên tia đối của tia EH . Lấy điểm K Sao cho EK = EH .Chứng minh Ak // BC
c Chứng minh HK = AB
d Gọi I là trung điểm của AH .Chứng minh 3 điểm B I K thẳng hàng
Cho tam giác ABC (AB < AC < BC), đường cao AH. Gọi D, E, F lần lượt là trung điểm của các cạnh AB, BC và AC. Gọi I là giao điểm của DF và AE.
b) Chứng I là trung điểm của DF.
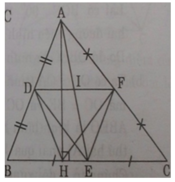
b) Ta có DF // BC (cmt) hay DI // BE; D là trung điểm của AD ⇒ I là trung điểm của AE và DI = BE/2
Trong ΔAEC có IF là đường trung bình nên IF = EC/2 mà EC = EB (gt) ⇒ IF = ID hay I là trung điểm của DF.
Đúng 0
Bình luận (0)
cho tam giác abc có ab ac, trên tia đối của tia ab lấy điểm m, trên tia đối của tia ac lấy điểm n sao cho am an. gọi i là trung điểm của bc, k là trung điểm của mncho tam giác abc có ab ac, trên tia đối của tia ab lấy điểm m, trên tia đối của tia ac lấy điểm n sao cho am an. gọi i là trung điểm của bc, k là trung điểm của mn1) Cm: tgiac abi tgiac aci 2) 3 điểm i,a,k thẳng hàngMN LÀM NHANH GIÚP MIK NHÉ, MIK CẦN GẤP LẮM R
Đọc tiếp
cho tam giác abc có ab = ac, trên tia đối của tia ab lấy điểm m, trên tia đối của tia ac lấy điểm n sao cho am = an. gọi i là trung điểm của bc, k là trung điểm của mncho tam giác abc có ab = ac, trên tia đối của tia ab lấy điểm m, trên tia đối của tia ac lấy điểm n sao cho am = an. gọi i là trung điểm của bc, k là trung điểm của mn
1) Cm: tgiac abi = tgiac aci
2) 3 điểm i,a,k thẳng hàng
MN LÀM NHANH GIÚP MIK NHÉ, MIK CẦN GẤP LẮM R
a) Xét ΔABCΔABC có:
AB=AC(gt)AB=AC(gt)
=> ΔABCΔABC cân tại A.
=> ˆABC=ˆACBABC^=ACB^ (tính chất tam giác cân).
Ta có:
{ˆABM+ˆABC=1800ˆACN+ˆACB=1800{ABM^+ABC^=1800ACN^+ACB^=1800 (các góc kề bù).
Mà ˆABC=ˆACB(cmt)ABC^=ACB^(cmt)
=> ˆABM=ˆACN.ABM^=ACN^.
Xét 2 ΔΔ ABMABM và ACNACN có:
AB=AC(gt)AB=AC(gt)
ˆABM=ˆACN(cmt)ABM^=ACN^(cmt)
BM=CN(gt)BM=CN(gt)
=> ΔABM=ΔACN(c−g−c)ΔABM=ΔACN(c−g−c)
=> AM=ANAM=AN (2 cạnh tương ứng).
b) Theo câu a) ta có AM=AN.AM=AN.
=> ΔAMNΔAMN cân tại A.
=> ˆM=ˆNM^=N^ (tính chất tam giác cân)
Xét 2 ΔΔ vuông BMEBME và CNFCNF có:
ˆMEB=ˆNFC=900(gt)MEB^=NFC^=900(gt)
BM=CN(gt)BM=CN(gt)
ˆM=ˆN(cmt)M^=N^(cmt)
=> ΔBME=ΔCNFΔBME=ΔCNF (cạnh huyền - góc nhọn)
Bài 10. Cho triangle ABC nhọn có AB = AC Gọi M là trung điểm của AB. a) Chứng minh tam giác AMB = tam giác AMC từ đó suy ra AM vuông góc BC b) Gọi I là trung điểm của AC. Trên tia đối của tia IB, lấy điểm N sao cho IN = IB. Chứng minh tam giâc IBC = tam giác INA và AN //BC. c) Gọi H là trung điểm của AN. Chứng minh H, I, M thẳng hàng.
a: Xét ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
=>ΔAMB=ΔAMC
=>góc AMB=góc AMC=180/2=90 độ
=>AM vuông góc BC
b: Xét ΔIBC và ΔINA có
IB=IN
góc BIC=góc NIA
IC=IA
=>ΔIBC=ΔINA
=>góc IBC=góc INA
=>BC//NA
Đúng 2
Bình luận (0)






