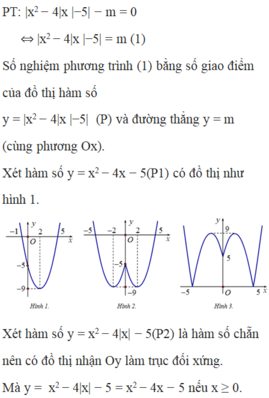
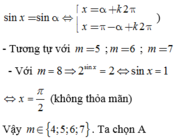Số nghiệm nguyên trong khoảng (-5;5) của bất phương trình \(\left|x+3\right|-\left|3-2x\right|\ge3x\)
TH
Những câu hỏi liên quan
1.Cho phương trình x2 +4x-m=0(1).Tìm tất cả các giá trị của tham số m để phương trinh (1) có đúng 1 nghiệm thuộc khoảng (-3,1)
2.Có bao nhiêu giá trị m nguyên trong nửa khoảng (0;2019] để phương trình |x2 -4|x|-5|-m có hai nghiệm phân biệt
Xét phương trình hoành độ giao điểm\(x^2\)+4x-m=0 <=> x^2+4x=m, đây là kết hợp của 2 hàm số (P):y=\(x^2\)+4x và (d):y=m.
Khi vẽ đồ thị ta thấy parabol đồng biến trên khoảng (-2;+∞)=> Điểm giao giữa parabol và đồ thị y=m là điểm duy nhất thỏa mãn phương trình có duy nhất 1 nghiệm thuộc khoảng (-3;1).Vậy để phương trình có 1 nghiệm duy nhất <=> delta=0 <=>16+4m=0<=>m=-4.
mình trình bày hơi dài mong bạn thông cảm 
Đúng 0
Bình luận (0)
Có bao nhiêu số nguyên m sao cho phương trình msinx + 4cosx = 4 có nghiệm trong khoảng (0;π/3)?
A. 2.
B. 3.
C. 4.
D. 5.
Số giá trị nguyên của tham số m nằm trong khoảng (0.2020) để phương trình
x
-
1
-
2019
-
x
2020
-
m
có nghiệm là A. 2020 B. 2021 C. 2019 D. 2018
Đọc tiếp
Số giá trị nguyên của tham số m nằm trong khoảng (0.2020) để phương trình x - 1 - 2019 - x = 2020 - m có nghiệm là
A. 2020
B. 2021
C. 2019
D. 2018
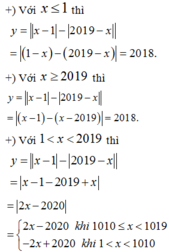
Do đó
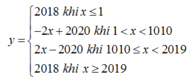
Vẽ dáng đồ thị hàm số ta được:
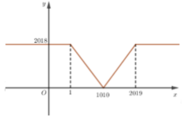
Từ hình vẽ ta thấy phương trình đã cho có nghiệm nếu đường thẳng y = 2020 - m cắt đồ thị hàm số trên tại ít nhất một điểm hay

giá trị của m thỏa mãn bài toán.
Chọn D.
Đúng 0
Bình luận (0)
Phương trình
l
o
g
2
(
5
-
2
x
)
2
-
x
có hai nghiệm
x
1
,
x
2
x
1
x
2
. Tổng các giá trị n...
Đọc tiếp
Phương trình l o g 2 ( 5 - 2 x ) = 2 - x có hai nghiệm x 1 , x 2 x 1 < x 2 . Tổng các giá trị nguyên trong khoảng x 1 ; x 2 bằng
A. 0
B. 3
C. 2
D. 1
Hỏi có bao nhiêu giá trị mm nguyên trong nửa khoảng (0; 2017] để phương trình | x 2 − 4|x |−5| − m = 0 có hai nghiệm phân biệt?
A. 2016
B. 2008
C. 2009
D. 2017
Thực nghiệm chỉ ra rằng các nguyên tử bền có tỉ lệ số nơtron/số proton nằm trong khoảng
1
≤
N
P
≤
1
,
5
(trừ trường hợp nguyên tử H). Một nguyên tử X bền có tổng số hạt (proton, nơtron, electron) là 13. X là nguyên tử của nguyên tố nào sau đây? A. liti B. beri C. cacbon D. nitơ
Đọc tiếp
Thực nghiệm chỉ ra rằng các nguyên tử bền có tỉ lệ số nơtron/số proton nằm trong khoảng 1 ≤ N P ≤ 1 , 5 (trừ trường hợp nguyên tử H). Một nguyên tử X bền có tổng số hạt (proton, nơtron, electron) là 13. X là nguyên tử của nguyên tố nào sau đây?
A. liti
B. beri
C. cacbon
D. nitơ
Tìm tổng các giá trị nguyên của tham số m để phương trình
4
sin
x
+
2
1
+
sin
x
m
có tổng các nghiệm trong khoảng
0
;
π
bằng
π
A. 22 B. 25 C. 30 D. 33
Đọc tiếp
Tìm tổng các giá trị nguyên của tham số m để phương trình 4 sin x + 2 1 + sin x = m có tổng các nghiệm trong khoảng 0 ; π bằng π
A. 22
B. 25
C. 30
D. 33
Tìm tổng các giá trị nguyên của tham số m để phương trình
4
sin
x
+
2
1
+
sin
x
m
có tổng các nghiệm trong khoảng
0
;
π
bằng
π
. A. 22 B. 25 C. 30 D. 33
Đọc tiếp
Tìm tổng các giá trị nguyên của tham số m để phương trình 4 sin x + 2 1 + sin x = m có tổng các nghiệm trong khoảng 0 ; π bằng π .
A. 22
B. 25
C. 30
D. 33
Đáp án A
Điều kiện x ∈ ℝ
Đặt t = 2 sin x . Phương trình đã cho trở thành t 2 + 2 t = m ( * )
Vì sin x = sin α ⇔ x = α + 2 k π x = π − α + k 2 π nên để phương trình đã cho có tổng các nghiệm trong khoảng 0 ; π bằng π thì phương trình (*) phải có đúng một nghiệm t ∈ 1 ; 2 sin x ∈ 0 ; 1 thì 2 sin x ∈ 1 ; 2
Xét hàm số f t = t 2 + 2 t có bảng biến thiên
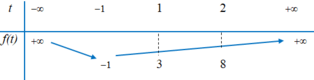
Suy ra để phương trình (*) có đúng một nghiệm t ∈ 1 ; 2 thì m ∈ 3 ; 8 .Vậy tổng các giá trị nguyên của m thỏa mãn yêu cầu bài toán là 4 + 5 + 6 + 7 = 22
Đúng 0
Bình luận (0)
Cho bất phương trình
2
log
3
2
(
3
x
)
-
2
m
log
3
x
+
3
log
2
x...
Đọc tiếp
Cho bất phương trình 2 log 3 2 ( 3 x ) - 2 m log 3 x + 3 log 2 x ( log 3 x + 2 - 2 m ) log 3 x ≤ 2 Biết rằng bất phương trình có đúng 74 nghiệm nguyên x ∈ 8 ; 2018 Giá trị nguyên của tham số m thỏa mãn bài toán nằm trong khoảng
A. (0;4)
B. (4;7)
C. (7;15)
D. (15;70)