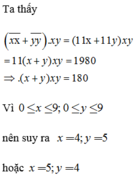Biến đổi đẳng thức đã cho về dạng:

(x+y)xy=180

Từ đây suy ra x=4, y=5 hoặc x=5, y=4

 1980=3.5.131 là tích 3 số nguyên tố 
vì x, y là chữ số nên chỉ có thể 
x=3, y=5 => xx=33, yy=55 hoặc ngược lại vai trò x,y 
=> (33+55).3.5=1320 không bằng 1980 
vậy không tồn tại x,y thỏa bài toán 

xx và yy có gạch ngang trên đầu nhé

Ta thấy: 

x x ¯ + yy ¯ . xy = ( 11 x + 11 y ) xy = 11 ( x + y ) xy = 1980 ⇒ . ( x + y ) xy = 180

Vì  0 ≤ x ≤ 9 ;   0 ≤ y ≤ 9 nên suy ra x = 4; y = 5 hoặc x= 5; y = 4

Cho mk hỏi đề bài:xx,yy,xy là các số nhân lại với nhau hay là 1 số tự nhiên

(11.x+11.y).xy=1980

11x^2y+11y^2x=1980

x^2y+y^2x=1980:11=180

x(xy+xy)=180

xx^2.y^2=180

180 phân h ra thừa số nguyên tố

la mot stn nha