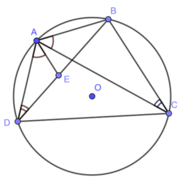
cho tứ giác abcd nội tiếp đt (o). cm rằng: AB.CD+BC.AD=AC.BD
NT
Những câu hỏi liên quan
Cho tứ giác ABCD nội tiếp đường tròn (O). Chứng minh AB.CD + BC.AD = AC.BD
Giả sử \(\widehat{ACB}>\widehat{ACD}\) trên BD lấy điểm E sao cho \(\widehat{BCE}=\widehat{ACD}\)
Xét △ACD và △BCE có
\(\widehat{BCE}=\widehat{ACD}\)(gt)
\(\widehat{CAD}=\widehat{CBE}\)(2 góc nội tiếp cùng chắn cung \(\stackrel\frown{CD}\))
Suy ra △ACD \(\sim\) △BCE(g-g)
\(\Rightarrow\frac{AC}{BC}=\frac{AD}{BE}\Rightarrow BC.AD=AC.BE\)(1)
Xét △ACB và △DCE có
\(\widehat{BCE}=\widehat{ACD}\Rightarrow\)\(\widehat{BCE}+\widehat{ECA}=\widehat{ACD}+\widehat{ECA}\Rightarrow\widehat{ACB}=\widehat{DCE}\)
\(\widehat{CDE}=\widehat{CAB}\)(2 góc nội tiếp cùng chắn cung \(\stackrel\frown{BC}\))
Suy ra △ACB \(\sim\) △DCE(g-g)
\(\Rightarrow\frac{AC}{DC}=\frac{AB}{DE}\Rightarrow AB.CD=AC.DE\)(2)
Cộng (1) và (2)\(\Leftrightarrow AB.CD+BC.AD=AC.BE+AC.DE=AC\left(BE+CE\right)=AC.BD\)
Vậy \(AB.CD+BC.AD=AC.BD\)
Đúng 0
Bình luận (0)
Cho tứ giác ABCD nội tiếp đường tròn (O) . Chứng minh rằng : AC.BD ≤ AB.CD + AD.BC .
Đây là đẳng thức ptôlêmê.
C/m: Lấy 1 điểm M thuộc AC sao cho gocABD=gocMBC. Do tứ giác ABCD nội tiếp nên ^ADC=^ACB. Từ 2 điều trên suy ra tam giác ABD ~ MBC(g.g). Suy ra AD/MC=BD/BC => AD.BC=BD.MC (1)
Từ cặp tam giác đồng dạng trên ta cũng có AB/BM = BD/BC => AB/BD = BM/BC mà ^ABM = ^DBC nên tam giác ABM ~ tam giác DBC.
=> AB.CD=AM.BD (2)
Cộng (1), (2) vế theo vế suy ra AC.BD = AB . CD + AD . BC
Vậy AC.BD = AB.CD + AD . BC ( đpcm )
Đúng 0
Bình luận (0)
cho tứ giác ABCD nội tiếp đường tròn (O). Chứng minh AB.CD+AD.BC=AC.BD
Ta có: `hat(ABD) = hat(ACD)`.
Lấy `M in AC` sao cho `hat(ADB) = hat(MDC)`.
`=> triangle ABD ~ triangle MCD`.
`=> (AB)/(MC) = (BD)/(CD) => AB . CD = BD . MC`.
Xét `2 triangle ADM, BDC`, ta có:
`hat(ADM) = hat(BDC)`.
`(DA)/(DM) = (BD)/(DC) ( triangle ABD ~ triangle MCD )`.
`=> triangle ADM ~ triangle BCD => (AD)/(AM) = (BD)/(CB) => AD . BC = BD . AM`
`=> AD . BC + AD . BC = BD . AM + BD . MC`
`=> AD . BC + AD . BC = BD(AM+MC)`
`=> AD.BC+AD.BC = BD . AC => dpcm`.
Đúng 3
Bình luận (3)
Cho tứ giác ABCD nội tiếp, AC cắt BD tại I, AD cắt BC tại J.
CMR: a) IA.IC=IB.ID
b) JA.ID=JB.JC
c) AB.CD+BC.AD=AC.BD
a) Xét \(\Delta IAD\)và \(\Delta IBC\)có:
\(\widehat{AID}=\widehat{BIC}\)(2góc đối đỉnh)
\(\widehat{ADI}=\widehat{BCI}\)(cùng nhìn cung AB)
\(\Rightarrow\Delta IAD\)đồng dạng với \(\Delta IBC\)
\(\Rightarrow\frac{IA}{IB}=\frac{ID}{IC}\Rightarrow IA.IC=IB.ID\)(ĐPCM)
b)Xét \(\Delta JAC\)và \(\Delta JBD\)có:
\(\widehat{J}\)là góc chung
\(\widehat{JCA}=\widehat{JDB}\)
\(\Rightarrow\)\(\Delta JAC\)đồng dạng với\(\Delta JBD\)
\(\Rightarrow\frac{JA}{JB}=\frac{JC}{JD}\Rightarrow JA.JD=JB.JC\)(ĐPCM)
Phần a tui đánh máy bị lỗi nhé, chỗ chữ bị nhỏ lên là góc á, còn đoạn gần cuối là \(\frac{IA}{IB}=\frac{ID}{IC}\)nhé
Xem thêm câu trả lời
cho tứ giác ABCD nội tiếp (o). Các tiếp tuyến tại A và C dồng qui với đường thẳng BD ở M. chứng minh: AB.CD=BC.AD
Cho tứ giác ABCD nội tiếp dường tròn (O). Chứng minh: AC.BD = AB.CD + AD.BC
Sao ko ai làm đ bài này trời ? hic.
Đúng 0
Bình luận (0)
vì tứ giác ABCD nội tiếp,theo định lý Ptoleme ta có:
AC.BD=AB.CD+AD.BC (ĐPCM)
Đúng 0
Bình luận (0)
Cho tứ giác ABCD nội tiếp đường tròn tâm ( O ) Chứng minh AB.CD+AD.BC=AC.BD
Cho tứ giác ABD nội tiếp trong vòng tròn (o). CM : AC.BD = AB.CD + AD.BC
Cho tứ giác ABCD nội tiếp đường tròn (O). Trên đường chéo BD lấy điểm E sao cho ∠ DAE = ∠ BAC . Chứng minh: AD.BC + AB.CD = AC.BD