Trong mặt phẳng tọa độ oxy, cho các điểm G(1;-2) và A thuộc Oy thỏa mãn G là trọng tâm của tam giác . Tọa độ véctơ 2AB là
KD
Những câu hỏi liên quan
Trong mặt phẳng tọa độ Oxy cho các điểm M(0; 4), N(–3; 2) và P(9; –3).
Tọa độ trọng tâm G của tam gác MNP là:
A. G(6; 3)
B. G(3;-1/2)
C. G(2; –1)
D. G(2; 1)
Tọa độ trọng tâm G của tam gác MNP là:
x G = x M + x N + x P 3 = 0 + ( − 3 ) + 9 3 = 2 y G = y M + y N + y P 3 = 4 + 2 + ( − 3 ) 3 = 1 ⇒ G ( 2 ; 1 )
Đáp án D
Đúng 0
Bình luận (0)
1. Trong mặt phẳng Oxy, có trọng tâm G(1,-1), M(2,1) và N(4,-2) lần lượt là trung điểm của AB, BC. Tìm tọa độ điểm B
2. Trong mặt phẳng Oxy, cho A(1,3), B(-2,2). Biết đường thẳng AB cắt trục tung tại điểm M(0,b). Giá trị b thuộc khoảng nào
3. Trong mặt phẳng tọa độ Oxy, cho A thỏa vecto OA 2vecto i + 3vecto j. Tọa độ điểm A là
4. Trong mặt phẳng Oxy, cho vecto x(1,2), vecto y(3,4), vecto z(5,-1). Tọa độ vecto u 2vecto x + vecto y - vecto z là
5. Trong mặt phẳng tọa độ Oxy, cho M(2,-3), N(4...
Đọc tiếp
1. Trong mặt phẳng Oxy, có trọng tâm G(1,-1), M(2,1) và N(4,-2) lần lượt là trung điểm của AB, BC. Tìm tọa độ điểm B
2. Trong mặt phẳng Oxy, cho A(1,3), B(-2,2). Biết đường thẳng AB cắt trục tung tại điểm M(0,b). Giá trị b thuộc khoảng nào
3. Trong mặt phẳng tọa độ Oxy, cho A thỏa vecto OA= 2vecto i + 3vecto j. Tọa độ điểm A là
4. Trong mặt phẳng Oxy, cho vecto x=(1,2), vecto y=(3,4), vecto z=(5,-1). Tọa độ vecto u = 2vecto x + vecto y - vecto z là
5. Trong mặt phẳng tọa độ Oxy, cho M(2,-3), N(4,7). Tọa độ trung điểm I của đoạn thẳng MN là
6. Cho vecto x=(-4,7) và hai vecto a=(2,-1), b=(-3,4). Nếu vecto x = m vecto a + n vecto b thì m, n là cặp số nào
Trong mặt phẳng tọa độ Oxy cho vectơ v = (2; −1) , điểm M = (3; 2). Tìm tọa độ của các điểm A sao cho: A = T v → ( M )
Giả sử A = (x; y). Khi đó

Vậy A = (5; 1)
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy cho vectơ v = (2; −1) , điểm M = (3; 2). Tìm tọa độ của các điểm A sao cho: M = T v → ( A )
Giả sử A = (x; y). Khi đó

Vậy A = (1; 3)
Đúng 0
Bình luận (0)
Cho các số phức
z
1
1
;
z
2
2
+
2
i
;
z
3
-
1
+
3
i
được biểu diễn trong mặt phẳn...
Đọc tiếp
Cho các số phức z 1 = 1 ; z 2 = 2 + 2 i ; z 3 = - 1 + 3 i được biểu diễn trong mặt phẳng tọa độ Oxy là M,N,P, các điểm này lần lượt là trung điểm của ba cạnh tam giác EFH. Tọa độ trọng tâm G của tam giác EFH là:
A. (2;3)
B. (3;2)
C. 2 3 ; 2 3
D. 2 3 ; 5 3
Chọn D.
M(1;0), N(2;2), P(-1;3) là điểm biểu diễn các số phức trên .
Hai tam giác EFH và MNP có 3 trung tuyến trùng nhau từng đôi một nên có cùng trọng tâm G.
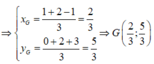
Đúng 0
Bình luận (0)
Cho các số phức
z
1
1
,
z
2
2
+
2
i
,
z
3
-
1
+
3
i
được biểu diễn trong mặt phẳng tọa độ Oxy là M,N,P , các điểm này lần lượt là trung điểm của ba cạnh tam giác EFH. Tọa độ trọng tâm G của tam giác EFH là: A.
2
;
3
B. ...
Đọc tiếp
Cho các số phức z 1 = 1 , z 2 = 2 + 2 i , z 3 = - 1 + 3 i được biểu diễn trong mặt phẳng tọa độ Oxy là M,N,P , các điểm này lần lượt là trung điểm của ba cạnh tam giác EFH. Tọa độ trọng tâm G của tam giác EFH là:
A. 2 ; 3
B. 3 ; 2
C. 2 3 ; 2 3
D. 2 3 ; 5 3
Trong mặt phẳng tọa độ Oxy cho các điểm A(3; 1); B(2; 2); C(1; 16); D(1; –6). Hỏi G(2; –1) là trọng tâm của tam giác nào trong các tam giác sau đây?
A. Tam giác ABD
B. Tam giác ABC
C. Tam giác ACD
D. Tam giác BCD
Trong mặt phẳng tọa độ Oxy cho đường thẳng d : y= x+2013. TÌm tọa độ giao điểm của đường thẳng với các trục tọa độ
Thay x=0 vào y=x+2013, ta được:
y=0+2013=2013
Thay y=0 vào y=x+2013, ta được:
x+2013=0
hay x=-2013
Đúng 1
Bình luận (0)
trong mặt phẳng tọa độ Oxy cho 2 điểm B(2;2), C(0;1). Tọa độ các điểm M nằm trên trục hoành thỏa MB = 2MC
\(\text{Đặt }M\left(x;y\right)\\ \overrightarrow{MB}\left(-2-x,2-y\right);\overrightarrow{MC}\left(-x,1-y\right)\\ \left|\overrightarrow{MB}\right|=\left|2\overrightarrow{MC}\right|\Leftrightarrow\sqrt{\left(-2-x\right)^2+\left(2-y\right)^2}=2\sqrt{\left(-x\right)^2+\left(1-y\right)^2}\\ \Leftrightarrow x^2+4x+4+y^2-4y+4=2x^2+2y^2-4y+2\\ \Leftrightarrow x^2+y^2-4y-6=0\\ \text{Mà }M\in Ox\Leftrightarrow y=0\Leftrightarrow x^2-6=0\Leftrightarrow\left[{}\begin{matrix}x=\sqrt{6}\\x=-\sqrt{6}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}M\left(\sqrt{6};0\right)\\M\left(-\sqrt{6};0\right)\end{matrix}\right.\)
Đúng 1
Bình luận (0)





