Cho hình vuông ABCD cạnh a. Tính
GH
Những câu hỏi liên quan
Cho hình chiếu ABCD ABCD là hình vuông cạnh a căn 2 SC vuông góc ABCD SC = 2a
a, tam giác SAC, SAB vuông
b tính SA(ABCD) , SA(SCD) , SB(SCD)
Xem chi tiết
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a SA vuông góc với ABCD Gọi P là trung điểm cạnh SD, PC = a căn(3). Tính thể tích hình chóp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA a
2
và vuông góc với (ABCD). Tính theo a thể tích V của khối chóp S.ABC A. V
2
6
a
3
B. V
2
2
3
a
3
C. V
2
a
3
D. V...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA = a 2 và vuông góc với (ABCD). Tính theo a thể tích V của khối chóp S.ABC
A. V = 2 6 a 3
B. V = 2 2 3 a 3
C. V = 2 a 3
D. V = 2 3 a 3
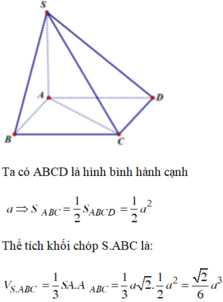
Chọn A.
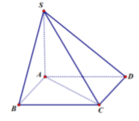
Ta có ABCD là hình bình hành cạnh a
![]()
Thể tích khối chóp S.ABC là:![]()
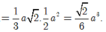
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với mặt đáy (ABCD), SC
a
5
. Tính thể tích khối chóp.
A
.
V
a
3
3
3
B
.
V
a
3...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với mặt đáy (ABCD), SC = a 5 . Tính thể tích khối chóp.
A . V = a 3 3 3
B . V = a 3 3 6
C . V = a 3 3
D . V = a 3 3 9
Đáp án A.
Ta có: ![]() (chiều cao của hình chóp)
(chiều cao của hình chóp)
Diện tích hình vuông ![]()
Thể tích khối chóp SABCD là: 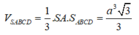
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên
S
A
a
2
và vuông góc với (ABCD). Tính theo a thể tích V của khối chóp S.ABC A.
V
2
6
a
3
B.
V
2
2
3
a...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên S A = a 2 và vuông góc với (ABCD). Tính theo a thể tích V của khối chóp S.ABC
A. V = 2 6 a 3
B. V = 2 2 3 a 3
C. a 3 2
D. V = 2 3 a 3
Cho hình chóp \(S.ABCD\) với đáy \(ABCD\) là hình vuông cạnh \(a\). Cho biết \(SA = a\) và \(SA\) vuông góc với \(\left( {ABCD} \right)\).
a) Tính khoảng cách từ điểm \(B\) đến \(\left( {SAD} \right)\).
b) Tính khoảng cách từ điểm \(A\) đến cạnh \(SC\).
a) Ta có:
\(\begin{array}{l}\left. \begin{array}{l}SA \bot \left( {ABCD} \right) \Rightarrow SA \bot AB\\AB \bot A{\rm{D}}\end{array} \right\} \Rightarrow AB \bot \left( {SA{\rm{D}}} \right)\\ \Rightarrow d\left( {B,\left( {SA{\rm{D}}} \right)} \right) = AB = a\end{array}\)
b) Kẻ \(AH \bot SC \Rightarrow d\left( {A,SC} \right) = AH\)
Tam giác \(ABC\) vuông tại \(B\)\( \Rightarrow AC = \sqrt {A{B^2} + B{C^2}} = a\sqrt 2 \)
Tam giác \(SAC\) vuông tại \(A\)\( \Rightarrow SC = \sqrt {S{A^2} + A{C^2}} = a\sqrt 3 \)
Tam giác \(SAC\) vuông tại \(A\) có đường cao \(AH\)\( \Rightarrow AH = \frac{{SA.AC}}{{SC}} = \frac{{a\sqrt 6 }}{3}\)
Vậy \(d\left( {A,SC} \right) = \frac{{a\sqrt 6 }}{3}\).
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với đáy (ABCD) và
S
C
a
5
. Tính thể tích khối chóp S.ABCD A.
V
a
3
3
3
.
B.
V
a
3
3...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với đáy (ABCD) và S C = a 5 . Tính thể tích khối chóp S.ABCD
A. V = a 3 3 3 .
B. V = a 3 3 6 .
C. V = a 3 3 .
D. V = a 3 15 3 .
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với đáy
A
B
C
D
và
S
C
a
5
. Tính thể tích khối chóp S.ABCD. A.
V
a
3
3
3
.
B.
V...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với đáy A B C D và S C = a 5 . Tính thể tích khối chóp S.ABCD.
A. V = a 3 3 3 .
B. V = a 3 3 6 .
C. V = a 3 3 .
D. V = a 3 15 3 .
Đáp án A
Tam giác SAC vuông tại A suy ra:
S A = S C 2 − A C 2 = a 5 2 − a 2 2 = a 3
Thể tích khối chóp S.ABCD là
V S . A B C D = 1 3 . S A . S S . A B C D = 1 3 . a 3 . a 2 = a 3 3 3
Đúng 0
Bình luận (0)
Hình vuông ABCD có cạnh 2cm.Hình vuông MNPQ có cạnh gấp 3 lần cạnh hình vuông ABCD.
a)Tính chu vi hình vuông MNPQ.
b)Chu vi hình vuông ABCD bằng một phần mấy chu vi hình vuông MNPQ ?
a) cạnh hình vuông MNPQ là 3x2=6(cm)
Chu vi MNPQ là 4x6=24
b) =1/3 nha
chúc bạn hoc tốt
HYC-25/1/2022
Cạnh hình vuông MNPQ :
2 x 3 = 6 ( cm )
Chu vi MNPQ :
4 X 6 = 24 ( cm )
b. 1/3
HT
Bài giải
a) Cạnh của hình vuông MNPQ là :
3 x 2 = 6 ( cm )
Chu vi hình vuông MNPQ là :
6 x 4 = 24 ( cm )
b) Chu vi hình vuông ABCD là :
2 x 4 = 8 ( cm )
Chu vi của hình vuông ABCD bằng số phần chu vi của hình vuông MNPQ là :
24 : 8 = \(\frac{1}{3}\)( phần )
Đáp số : \(\frac{1}{3}\)phần.
Xem thêm câu trả lời