Bài toán được mô tả bằng hình vẽ bên cạnh .
a) tính AH, AB,AC
b) Tính sin IAK, cos IAK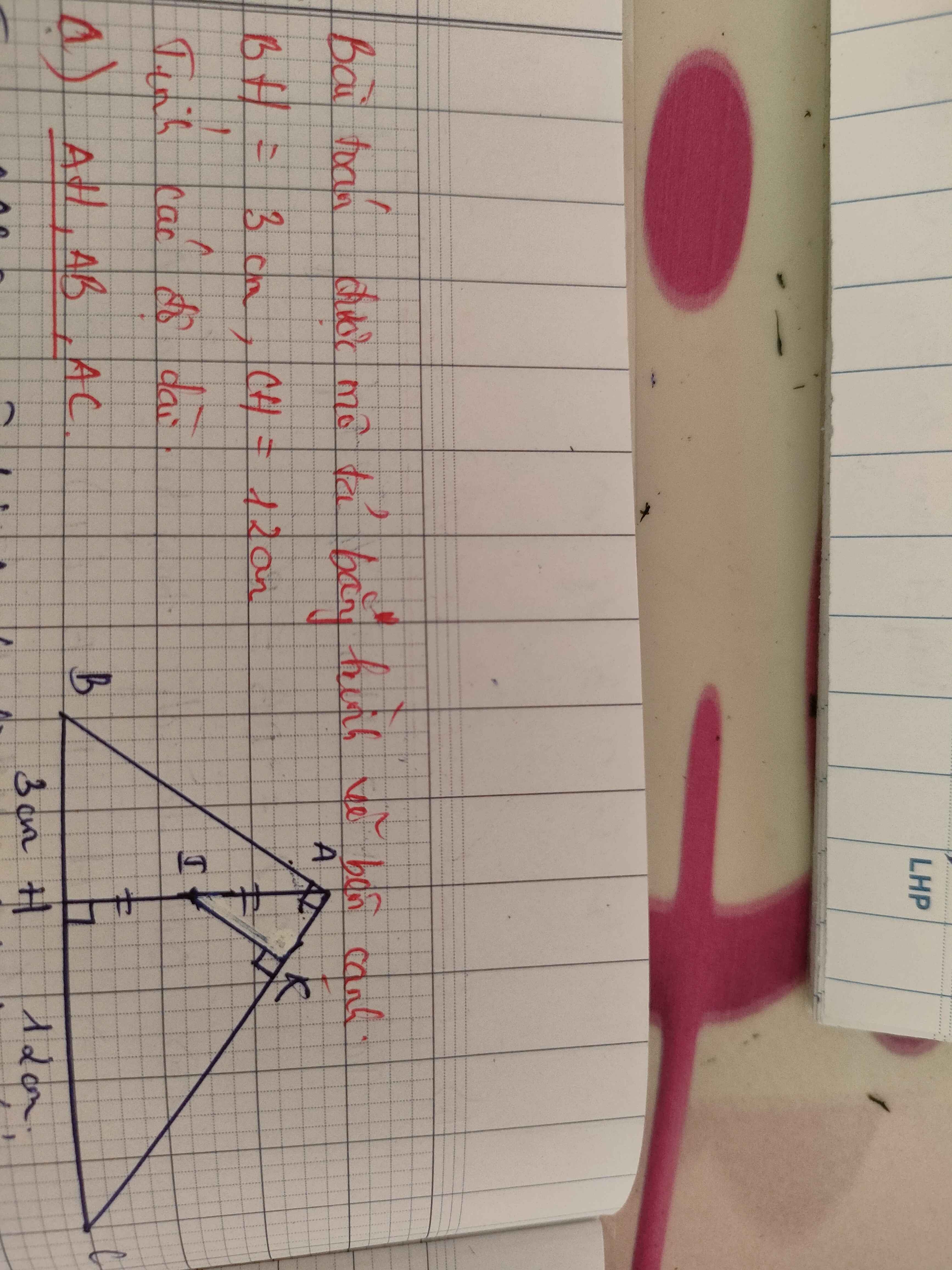
CH
Những câu hỏi liên quan
Bài 1: cho hình thang ABCD có 2 cạnh bên AD và BC bằng nhau, đường chéo AC vuông góc với BC biết AD5a, AC12aa) tính frac{sin B+cos B}{sin B-cos B}b)tính chiều cao của hình thang ABCDBài 2: cho tam giác cân ABC có AB AC 10cm, BC 16cm, trên đường cao AH lấy I sao cho AI 1/3 AH. Kẻ CX song song với AH, CX cắt BI tại D.a) tính các góc của tam giác ABCb) tính diện tích ABCDBài 3: cho hình thang đáy nhỏ 15 cm, 2 cạnh bên bằng nhau và bằng 25cm, góc tù là 120 độ. tính chu vi và diện tích
Đọc tiếp
Bài 1: cho hình thang ABCD có 2 cạnh bên AD và BC bằng nhau, đường chéo AC vuông góc với BC biết AD=5a, AC=12a
a) tính \(\frac{\sin B+\cos B}{\sin B-\cos B}\)
b)tính chiều cao của hình thang ABCD
Bài 2: cho tam giác cân ABC có AB = AC =10cm, BC = 16cm, trên đường cao AH lấy I sao cho AI= 1/3 AH. Kẻ CX song song với AH, CX cắt BI tại D.
a) tính các góc của tam giác ABC
b) tính diện tích ABCD
Bài 3: cho hình thang đáy nhỏ 15 cm, 2 cạnh bên bằng nhau và bằng 25cm, góc tù là 120 độ. tính chu vi và diện tích
Cho hình thang ABCD có hai cạnh bên là AD và BC bằng nhau, đường chéo AC vuông góc với cạnh bên BC. Biết AD = 5a, AC = 12 a
a) Tính :
\(\dfrac{\sin B+\cos B}{\sin B-\cos B}\)
b) Tính chiều cao của hình thang ABCD
a, \(\Delta ABC\) có \(\widehat{C}=90^o\).
Áp dụng pytago có: \(AB=\sqrt{AC^2+BC^2}=\sqrt{\left(12a\right)^2+\left(5a\right)^2}=13a\)
\(\Delta ABC\) có \(\widehat{C}=90^o\)\(\Rightarrow\)\(\left\{{}\begin{matrix}\sin B=\dfrac{AC}{AB}=\dfrac{12a}{13a}=\dfrac{12}{13}\\cosB=\dfrac{BC}{AB}=\dfrac{5a}{13a}=\dfrac{5}{13}\end{matrix}\right.\)
Ta có: \(\dfrac{sinB+cosB}{sinB-cosB}=\dfrac{\dfrac{12}{13}+\dfrac{5}{13}}{\dfrac{12}{13}-\dfrac{5}{13}}=\dfrac{\dfrac{17}{13}}{\dfrac{7}{13}}=\dfrac{17}{7}\)
b, Có SABCD= \(\dfrac{CH.AB}{2}=\dfrac{CB.AC}{2}\Rightarrow CH.AB=BC.AC\Rightarrow CH=\dfrac{AC.BC}{AB}=\dfrac{12a.5a}{13a}=\dfrac{60a}{13}\approx4,615a\)
Đúng 0
Bình luận (0)
Vẽ tam giác ABC vuông tại A, đường cao AH. Tính BC, AH, BH, CH, \(\cos B,\cos C,\sin B,\sin C\). Biết AB = 6 cm, \(\frac{AC}{AB}=\sqrt{3}\)
1. Cho tam giác ABC vuông tại A, đường cao AH, biết AB=4cm,AC=9cm. Tính sin B, sin C
2.Cho tam giác ABC vuông tại A, Cos B= an pha, Cos = 4/5. Tính sin, tan,cos
3. Cho tam giác ABC vuông tại A, đường cao AH, biết AB=6cm, BC= 10cm
a. Tính AC,AH. Tỉ số đồng giác góc B,C
b. Gọi E,F lần lượt là hình chiếu H lên AB,AC. CM :AE.AD=AF.AC
c. Tính S tứ giác AEHF
Cho hình vuông ABCD có cạnh bằng 12 cm. Trên cạnh AB lấy điểm
M sao
cho AM = 3BM. Trên cạnh BC lấy điểm N sao cho BN = 2CN. Trên cạnh AD lấy
điểm I sao cho DI = 2AI.
a) Tính diện tích tam giác MNI.
b) Đường chéo AC cắt NI tại trung điểm O của mỗi đường; IM cắt AC tại K. Tính
diện tích tam giác IAK
TTôi từng nghe:Trong "Principia Mathematica" của Bertrand Russell và Alfred North Whitehead, việc chứng minh 1 + 1 = 2 mất khoảng 362 trang. Đây là một phần của nỗ lực xây dựng toán học dựa trên logic hình thức. Chứng minh này phản ánh sự phức tạp của các định nghĩa và tiên đề trong lý thuyết tập hợp và số học. Nếu bạn cần thêm thông tin về nội dung cụ thể, hãy cho tôi biết! Chứng minh 1 + 1 = 2 trong "Principia Mathematica" được xem là khó khăn vì nó yêu cầu hiểu biết sâu sắc về logic hình thức và các định nghĩa phức tạp. Mặc dù kết quả cuối cùng có vẻ đơn giản, quá trình chứng minh đòi hỏi nhiều bước logic và khái niệm toán học. Nếu bạn không quen với lý thuyết này, nó có thể khá trừu tượng và khó tiếp cận.
Đúng 1
Bình luận (0)
Tôi từng nghe:Trong "Principia Mathematica" của Bertrand Russell và Alfred North Whitehead, việc chứng minh 1 + 1 = 2 mất khoảng 362 trang. Đây là một phần của nỗ lực xây dựng toán học dựa trên logic hình thức. Chứng minh này phản ánh sự phức tạp của các định nghĩa và tiên đề trong lý thuyết tập hợp và số học. Nếu bạn cần thêm thông tin về nội dung cụ thể, hãy cho tôi biết! Chứng minh 1 + 1 = 2 trong "Principia Mathematica" được xem là khó khăn vì nó yêu cầu hiểu biết sâu sắc về logic hình thức và các định nghĩa phức tạp. Mặc dù kết quả cuối cùng có vẻ đơn giản, quá trình chứng minh đòi hỏi nhiều bước logic và khái niệm toán học. Nếu bạn không quen với lý thuyết này, nó có thể khá trừu tượng và khó tiếp cận.
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho hình vuông ABCD có cạnh bằng 12 cm. Trên cạnh AB lấy điểm
M sao
cho AM = 3BM. Trên cạnh BC lấy điểm N sao cho BN = 2CN. Trên cạnh AD lấy
điểm I sao cho DI = 2AI.
a) Tính diện tích tam giác MNI.
b) Đường chéo AC cắt NI tại trung điểm O của mỗi đường; IM cắt AC tại K. Tính
diện tích tam giác IAK
Cho hình thang ABCD có cạnh bên AD=BC, đường chéo AC\(⊥\)BC biết AD=5a, AC=12a.
a) Tính \(\frac{\sin B+\cos B}{\sin B-\cos B}\)
b) Tính \(S_{ABCD}\)
do AD=CB=5a
trong tam giac ACB vuong co
\(\tan B=\frac{AC}{CB}=\frac{12}{5}\)
MA \(\frac{\sin B+\cos B}{\sin B-\cos B}=\frac{\frac{\sin B}{\cos B}+1}{\frac{\sin B}{\cos B}-1}=\frac{\tan B+1}{\tan B-1}=\frac{\frac{12}{5}+1}{\frac{12}{5}-1}=\frac{17}{7}\)
Đúng 0
Bình luận (0)
Một hình A được ghép từ một hình tam giác cân, với đương cao a,cạnh bên b và một hình bán nguyệt với bán kính a như hình vẽ.Hãy mô tả thuật toán tính diện tích hình A
Cho hình thang ABCD có hai cạnh bên là AD và BC bằng nhau, đường chéo AC vuông góc với cạnh bên BC. Biết AD = 5a, AC = 12a.
a) Tính (sin B + cos B)/(sin B - cos B)b) Tính chiều cao của hình thang ABCD.Giúp mình với! Cảm ơn!