Cho hình vẽ bên. Chứng minh rằng:
a) MNQ =PQN;
b) MN song song với PQ ;
c) MQ song song với NP ; 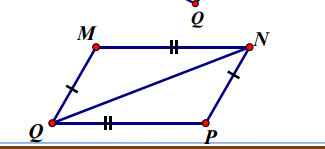
Cho Hình 3.30, biết các góc MNQ và PQN có cùng số đo bằng 35 \(^\circ \).
Chứng tỏ MN // QP.
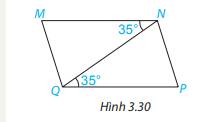
Vì \(\widehat {MNQ} = \widehat {PQN}( = 35^\circ )\), mà hai góc này ở vị trí so le trong nên MN // QP. (Dấu hiệu nhận biết hai đường thẳng song song)
vì góc MNQ và NQP là e góc solo trong bằng nhau
su ra MN//QP
Cho hình vẽ bên, biết góc NMP=110 độ, góc MPQ= 70 độ, góc MNQ= 125 độ
a) Chứng minh x//y
b) Tính số đo của góc Q1 ?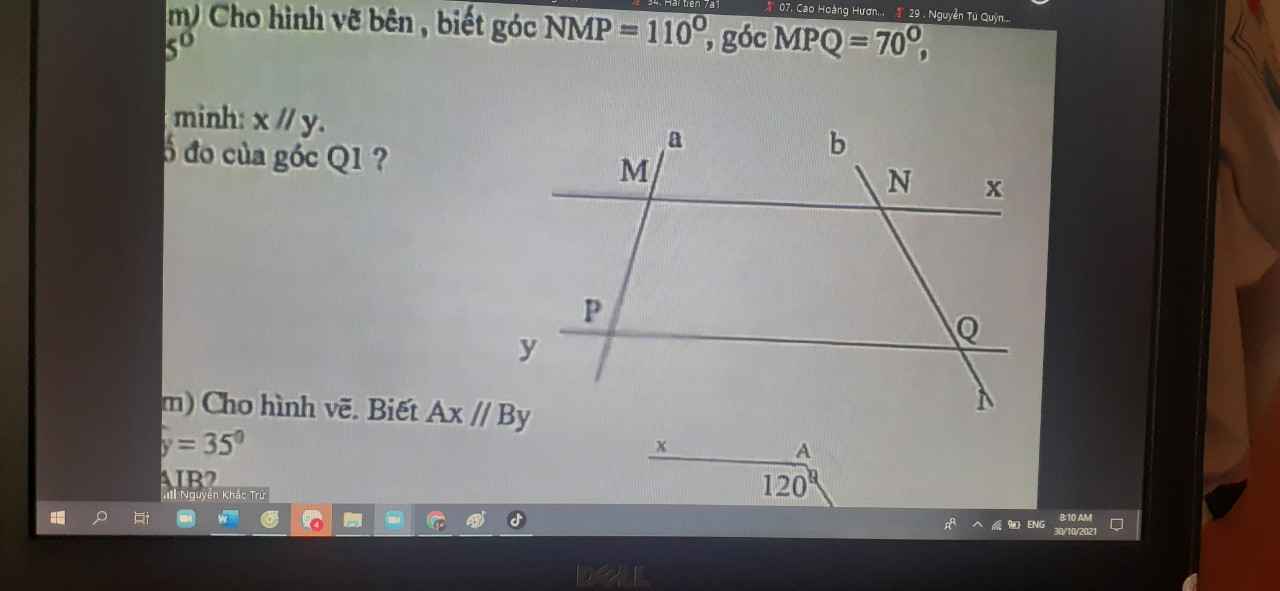
Trong hình vẽ bên, cho ABC ̂ = 800, By là tia phân giác của ABC ̂.
Chứng minh rằng:
a) Ax ⫽ By theo hai cách b) Ax ⫽ Cz
Cho hình vẽ bên, trong đó MP song song với NQ. Trên nửa mặt phẳng không chứa điểm P có bờ là đường thẳng MN, vẽ
điểm E sao cho E M N ^ = M N Q ^ . Chứng minh các điểm E, M, P thẳng hàng.
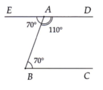
Cho Hình vẽ sau trong đó PNQ > PQN chứng minh :
A) PQ > PN
B) KQ > KN
Cho hình chóp \(S.ABCD\) có các cạnh bên bằng nhau và đáy là hình vuông. Chứng minh rằng:
a) \(\left( {SAC} \right) \bot \left( {ABCD} \right)\);
b) \(\left( {SAC} \right) \bot \left( {SBD} \right)\).
Gọi O là tâm của hình vuông ABCD
=>O là trung điểm chung của AC và BD
a:S.ABCD là hình chóp tứ giác đều nên SO vuông góc (ABCD)
mà \(SO\subset\left(SAC\right)\)
nên \(\left(SAC\right)\perp\left(ABCD\right)\)
b: BD vuông góc SO
BD vuông góc AC
\(SO,AC\subset\left(SAC\right)\)
=>\(BD\perp\left(SAC\right)\)
=>\(\left(SAC\right)\perp\left(SBD\right)\)
Cho tứ giác ABCD thỏa mãn AB = CD, AD = BC. Chứng minh rằng:
a, △ABC = △CDA
b, AB // CD và AD // BC
~Có vẽ hình~
b: Xét tứ giác ABCD có
AB=CD
AD=BC
Do đó: ABCD là hình bình hành
Suy ra: AB//CD;AD//BC
Cho tam giác MNQ vuông tại M. Vẽ MI vuông góc QN.
a) Chứng minh góc MNI = IMQ
b) Vẽ NK là tia phân giác của góc MNQ, vẽ QK là tia phân giác của góc MQN. Tính góc NKQ.
cho hình vẽ,biết góc M1 và N1=125 độ,Q1=75 độ
a,vẽ hình ,ghi gt-kl
b chứng minh x//y
c tính m2,p1,p2
d, kẻ tia phân giác mt của pmn cắt tia phân giác nz của mnq tại k.tính số đo mkn