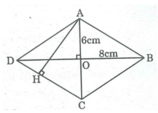
ABCD là hình thoi có O là giao điểm của hai đường chéo nên:

AO = OC = 6cm; OB = OD = 8cm

Trong tam giác vuông OAB, ta có:

A B 2 = O A 2 + O B 2 = 6 2 + 8 2  = 100

AB = 10 (cm)

Kẻ AH ⊥ CD (H ∈ CD)

Ta có: S A B C D  = AH.CD ⇒ AH =  S A B C D  / CD = 96/10 = 9,6 (cm)

Độ dài cạnh là \(\sqrt{41}\left(cm\right)\)

Gọi hình thoi đó là ABCD

Hai đường chéo BD và AC cắt nhau và vuông góc tại O

Kẻ đường cao AH (H\(\in DC\))

a. S_ABCD=\(\dfrac{1}{2}.AC.BD=\dfrac{1}{2}.12.16=96\left(cm^2\right)\)

Vậy diện tích hình thoi đó là 96 cm²

b. Ta có: AO=OC=\(\dfrac{AC}{2}=\dfrac{12}{2}=6\left(cm\right)\)

OD=OB=\(\dfrac{BD}{2}=\dfrac{16}{2}=8\left(cm\right)\)

Xét \(\Delta DAO\) có \(\widehat{DOA}=90^o\)

=> OD²+AO²=AD² (định lý Py-ta-go)

hay: 8²+6²=AD²

=> AD²=100

=> AD=10 (cm)

Vậy độ dài một cạnh của hình thoi đó là 10 cm

c. Ta có: S_ABCD=AH.DC

=> AH=\(\dfrac{S_{ABCD}}{DC}=\dfrac{96}{10}=9,6\left(cm\right)\)

Vậy độ dài đường cao của hình thoi đó là 9,6 cm

Gọi hình thoi đó là \(ABCD\)

Hai đường chéo BD và AC cắt nhau và vuông góc tại O

Kẻ đường cao AH \(\left(H\in DC\right)\)

a ) \(S_{ABCD}=\frac{1}{2}.AC.BD=\frac{1}{2}.12.16=96\left(cm^2\right)\)

Vậy diện tích hình thoi đó là \(96cm^2\)

b ) Ta có : \(AO=OC=\frac{AC}{2}=\frac{12}{2}=6\left(cm\right)\)

\(OD=OB=\frac{BD}{2}=\frac{16}{2}=8\left(cm\right)\)

Xét \(\Delta DAO\)có \(\widehat{DOA}=90^0\)

\(\Rightarrow OD^2+AO^2=AD^2\)( định lí Py - ta - go )

Hay \(8^2+6^2=AD^2\)

\(\Rightarrow AD^2=100\)

\(\Rightarrow AD=10\left(cm\right)\)

Vậy độ dài một cạnh của hình thoi đó là 10 cm

c ) Ta có : \(S_{ABCD}=AH.DC\)

\(\Rightarrow AH=\frac{S_{ABCD}}{DC}=\frac{96}{10}=9,6\left(cm\right)\)

Vậy độ dài dduwowgf cao của hình thoi là 9,6 cm

Chúc bạn học tốt !!!

Vì ABCD là hình thoi nên \(AB=BC=CD=DA=20\left(cm\right)\)

Và AC cắt BD tại O nên O là trung điểm AC,BD

\(\Rightarrow AC=2AO=32\left(cm\right);BD=2OB=24\left(cm\right)\)

OB = 12 cm => BD = 2.12 = 24 cm

OA = 16 cm => AC = 2.16 = 32 cm

AB = BC = CD = AD = 20 cm (hình thoi có 4 cạnh bằng nhau)

Đáp án D

Chọn câu D:96

đáo án : D

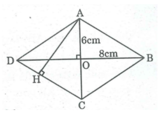
Ta có: S A B C D  = 1/2 AC.BD = 1/2 .12.16 = 96 ( c m 2 )