Cho hình bình hành ABCD,cạnh AB=a.AD=b .Tính AC^2+BD^2 theo a và b
TB
Những câu hỏi liên quan
Cho hình bình hành ABCD,cạnh AB=a.AD=b .Tính AC^2+BD^2 theo a và b
Lời giải:
\(AC^2+BD^2=(\overrightarrow{AC})^2+(\overrightarrow{BD})^2\)
\(=(\overrightarrow{AB}+\overrightarrow{AD})^2+(\overrightarrow{BA}+\overrightarrow{BC})^2\)
\(=AB^2+AD^2+AB^2+BC^2+2\overrightarrow{AB}.\overrightarrow{AD}+2\overrightarrow{BA}.\overrightarrow{BC}\)
\(=2(a^2+b^2)+2\overrightarrow{AB}.\overrightarrow{AD}-2\overrightarrow{AB}.\overrightarrow{AD}=2(a^2+b^2)\)
Đúng 1
Bình luận (0)
Cho tứ giác ABCD có E, F, G, H theo thứ tự là trung điểm của các cạnh AB, BC, CD, DA. a) Chứng minh tứ giác EFGH là hình bình hành. b) Cho AC= 6cm; BD=8cm. Tính độ dài các cạnh của hình bình hành EFGH. 2 Giải giúp mình với
a: Xét ΔABC có
E là trung điểm của AB
F là trung điểm của BC
Do đó: EF là đường trung bình
=>EF//AC và EF=AC/2(1)
Xét ΔCDA có
G là trung điểm của CD
H là trung điểm của DA
Do đó: GH là đường trung bình
=>GH//AC và GH=AC/2(2)
Từ (1) và (2) suy ra EF//GH và EF=GH
hay EFGH là hình bình hành
b: EF=GH=AC/2=3(cm)
FG=EH=BD/2=4(cm)
Đúng 2
Bình luận (0)
1,Cho hình thang ABCD,2 cạnh đáy AB và CD.2 đường chéo cắt nhau tại O.biết rằng OA=2cm,OC=6cm,OB=4cm.OD?
2,cho hình bình hành ABCD.Cac điểm M,N lần lượt thuộc cạnh AB và CD sao cho AM=CN.Chứng minh
a,AMCN là hình bình hành
b,3 đường thẳng AC,BD,MN đồng quy
3.Cho tứ giác ABCD có AB vuông góc với BD,AC vuông góc với CD.2 đường chéo cắt nhau tại I.chứng minh IA.IC=IB.ID
Cho tứ giác ABCD gọi E,F,G,H lần lượt là trung điểm của AB,BC,CD,DA
a,Chứng minh rằng EFGH là hình bình hành
b,Cho AC=8cm và BD=6cm .Hãy tính các cạnh của hình bình hành và chu vi của hình bình hành đó
a: Xét ΔABC có
E là trung điểm của AB
F là trung điểm của BC
Do đó: EF là đường trung bình của ΔBAC
Suy ra: EF//AC và \(EF=\dfrac{AC}{2}\left(1\right)\)
Xét ΔADC có
H là trung điểm của AD
G là trung điểm của CD
Do đó: HG là đường trung bình của ΔADC
Suy ra: HG//AC và \(HG=\dfrac{AC}{2}\left(2\right)\)
Từ (1) và (2) suy ra EF//HG và EF=HG
Xét tứ giác EFGH có
EF//HG
EF=HG
Do đó: EFGH là hình bình hành
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD. Phía trong hình bình hành dựng các tia Ax, By, Cz, Dt theo thứ tự tạo với các cạnh AB, BC, CD, DA.Các goc bằng nhau và cắt nhau tại M,N,P,Q
Chứng minh: a, MNPQ là hình bình hành
b, MP, NQ, AC, BD đồng quy
Cho hình bình hành ABCD, với diện tích S và AB = a, AD = b. Lấy mỗi cạnh của hình bình hành đó làm cạnh dựng một hình vuông ra phía ngoài hình bình hành. Tính theo a, b và S diện tích của đa giác giới hạn bởi các cạnh của hình vuông mà không là cạnh của hình bình hành đã cho.
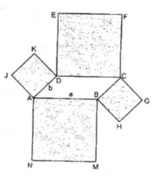
Hình đa giác đó gồm hình bình hành ABCD, hình vuông ABMN, BHGC, CFED, DKJA.
S A B M N = S C D E F = a 2
S B H G C = S D K J A = b 2
Diện tích đa giác bằng :
S A B M N = S C D E F = a 2
S B H G C = S D K J A = b 2
Đúng 1
Bình luận (0)
cho tứ giác ABCD. Gọi E,F,G,H theo thứ tự là trung điểm BD,AB,AC,CD
A) chứng minh EFGH là hình bình hành
b) cho AD=a, BC=b. Tính chu vi hình bình hành EFGH
a) Xét tam giác DBC có :
E là trung điểm của BD ( gt )
H là trung điểm của CD ( gt )
=> EH là đường trung bình của ΔDBC.
=> EH // BC và \(EH=\frac{1}{2}BC\) (1).
Xét tam giác ABC có :
F là trung điểm của AB ( gt )
G là trung điểm của AC ( gt )
=> FG là đường trung bình của ΔABC..
=>FG // BC và \(FG=\frac{1}{2}BC\) (2)
Từ ( 1 ) và ( 2 ) suy ra : FG // EH // BC và EH = FG
Vậy EFGH là hình bình hành
b, Theo ( 1) ta có : \(EH=\frac{1}{2}BC\)
mà bài cho BC = b
=> EH = \(\frac{b}{2}\)
Xét tam giác ABD có :
F là trung điểm của AB ( gt )
E là trung điểm của BD ( gt )
=> FE là đường trung bình của tam giác ABD
=> FE =\(\frac{1}{2}AD=\frac{a}{2}\) ( vì bài cho AD = a )
Chu vi hình bình hành EFGH là :
\(P_{EFGH}=2.\left(\frac{b}{2}+\frac{a}{2}\right)=a+b\)
Vậy chu vi hình thang EFGH = a + b hay = AD + BC .
Cho hình thoi ABCD, hình bình hành ABEC và hình chữ nhật BEFD.Biết DC=5cm, AC= 8cm, BD= 6cm
a)Tính độ dài cạnh BE và cạnh CE.
b)Tính chu vi ABEFD.
CẦN GẤP AA
Để chứng minh a. ON//(SAB) và b. (OMN)//(SCD), chúng ta có thể sử dụng các định lý và quy tắc trong hình học không gian.
a. Để chứng minh ON//(SAB), ta có thể sử dụng định lý về đường thẳng song song trong hình học không gian. Theo định lý này, nếu có hai đường thẳng cắt một mặt phẳng và các đường thẳng này đều song song với một đường thẳng thứ ba trong mặt phẳng đó, thì hai đường thẳng đó cũng song song với nhau. Áp dụng định lý này, ta có thể chứng minh ON//(SAB) bằng cách chứng minh rằng ON và AB đều song song với một đường thẳng thứ ba trong mặt phẳng chứa chóp S.ABCD.
b. Để chứng minh (OMN)//(SCD), ta cũng có thể sử dụng định lý về đường thẳng song song trong hình học không gian. Tương tự như trường hợp trước, ta cần chứng minh rằng OM và CD đều song song với một đường thẳng thứ ba trong mặt phẳng chứa chóp S.ABCD.
Tuy nhiên, để chứng minh chính xác các phần a và b, cần có thêm thông tin về các góc và độ dài trong hình chóp S.ABCD.
Đúng 0
Bình luận (0)
Tứ giác ABCD, gọi E;F;G;H theo thứ tự là trung điểm củ BD; AB; AC; CD
a) CM: EFGH là hình bình hành
b) Cho AD = a; BC = b. Tính chu vi của hình bình hành EFGH


