NI
Những câu hỏi liên quan
Câu 11: Biết x o ; y o ; z o là nghiệm nguyên dương của phương trình x 2 + y 2 + z 2 = xy + 3y + 2x
- 4. Khi đó x o + y o + z o = .....
Gọi (xo;yo;zo) là nghiệm của hệ \(\{\begin{matrix} x+y+2z=4 \\ 2x-y+3z=6 \\ x-3y+4z=7 \end{matrix}\)
Khi đó xo+yo+zo= ...?
nếu hai góc nhọn xoy và x'o'y' có ox// với o'x' oy// với o'y' thì xoy = x'o'y'
tìm y
y x 8 +y : 0,5 = 100
y x 56 + y : 0,25
ai nhanh giúp mình với
:o :o :o :o
CMR: Nếu 2 góc nhọn xOy và x'O'y' có Ox//O'x' Oy//O'y' thì góc xOy = góc x'O'y'
chứng minh rằng "nếu hai góc nhọn xOy và x'O'y'có Ox//O'x' Oy//O'y' thì xOy = x'O'y' (O' nằm trong góc xOy )
Cho hình vẽ
O'x' // Ox , O'y cắt Ox tại k . tính x'O'y' và x'O'k theo O
cân bằng PTHH:
d) Fe x O y + HNO 3 → Fe(NO 3 ) 3 + NO + H 2 O
e) Fe x O y + HNO 3 → Fe(NO 3 ) 3 + NO 2 + H 2
f) Fe x O y + HCl → FeCl 2y/x + H 2 O
g) Fe x O y + H 2 SO 4 → Fe 2 (SO 4 ) 2y/x + H 2 O
Cho 2 góc tù Xoy và x'o'y' như hình bẽ bên,trong đó ox//o,x',oy//o'y'.Chứng minh rằng xoy = x'o'y'
Cho hai góc nhọn xOy và x'O'y' có các cạnh tương ứng Ox // O'x' , Oy // O'y'. Vẽ các tia Oz và O'z' lần lượt là phân giác của góc xOy và x'O'y'. Chứng tỏ :
a) Hai góc xOy và x'O'y' bằng nhau.
b) Oz // O'z'.
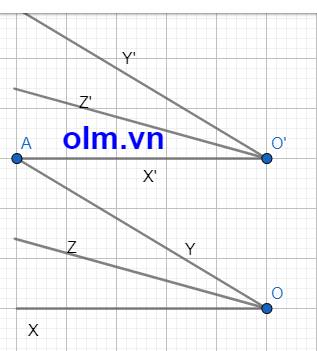
a,Kéo dài OY cắt O'X' tại A ta có:
\(\widehat{XOY}\) = \(\widehat{XOA}\) = \(\widehat{OAO'}\) (so le trong) (1)
\(\widehat{Y'O'X'}\) = \(\widehat{Y'O'A}\) = \(\widehat{OAO'}\) (so le trong) (2)
Kết hợp (1) Và (2) ta có:
\(\widehat{XOY=}\) \(\widehat{X'O'Y'}\) (đpcm)
Đúng 0
Bình luận (0)
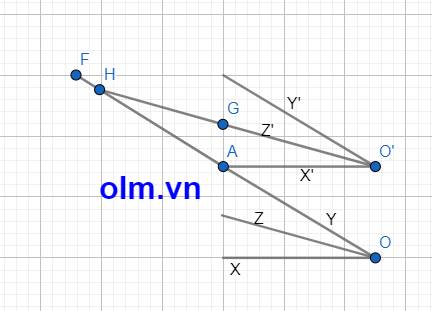
b, Kéo dài OY cắt O'Z' tại H
\(\widehat{ZOA}\) = \(\dfrac{1}{2}\) \(\widehat{XOY}\) (vì OZ là phân giác của góc XOY
\(\widehat{HO'A}\) = \(\dfrac{1}{2}\) \(\widehat{X'O'Y'}\) (vì OY là phân giác của góc X'O'Y')
Mặt khác ta có \(\widehat{OAO'}\) = \(\widehat{HO'A}\) + \(\widehat{AHO'}\) (góc ngoài tam giác bằng tổng hai góc trong không kề với nó)
\(\widehat{HO'A}\) = \(\dfrac{1}{2}\) \(\widehat{OAO'}\) ⇒ \(\widehat{AHO'}\) = \(\dfrac{1}{2}\) \(\widehat{OAO'}\) = \(\dfrac{1}{2}\) \(\widehat{XOY}\)
⇒ \(\widehat{ZOA}\) = \(\widehat{AHO'}\) (hai góc này ở vị trí so le trong)
⇒ OZ // O'Z' (đpcm)
Đúng 0
Bình luận (0)


