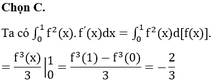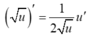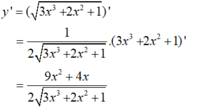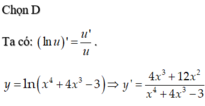y(4x3−2x2+1)2014y(4x3−2x2+1)2014. Đạo hàm y′y′ là:
Đọc tiếp
y=(4x3−2x2+1)2014. Đạo hàm y′ là:
TL
Những câu hỏi liên quan
Bài 1:Thực hiện các phép tính
a. (x5 +4x3 - 6x2):4x2
b. (x3 +x2-12) : (x-2)
c. (-2x5+3x2-4x3):2x2
d. (x3 - 64):(x2 + 4x + 16)
Bài 2:Rút gọn biểu thức
a. 3x (x - 2)- 5x (1 - x) - 8(x2 - 3)
b.(x - y) (x2 + xy + y2)+2y3
c. (x - y)2 + (x+y)2 - 2(x-y) (x+y)
Đọc tiếp
Bài 1:Thực hiện các phép tính
a. (x5 +4x3 - 6x2):4x2
b. (x3 +x2-12) : (x-2)
c. (-2x5+3x2-4x3):2x2
d. (x3 - 64):(x2 + 4x + 16)
Bài 2:Rút gọn biểu thức
a. 3x (x - 2)- 5x (1 - x) - 8(x2 - 3)
b.(x - y) (x2 + xy + y2)+2y3
c. (x - y)2 + (x+y)2 - 2(x-y) (x+y)
a) \(\left(x^5+4x^3-6x^2\right):4x^2\)
\(=\left(x^5:4x^2\right)+\left(4x^3:4x^2\right)+\left(-6x^2:4x^2\right)\)
\(=\dfrac{1}{4}x^3+x-\dfrac{3}{2}\)
b)
Vậy \(\left(x^3+x^2-12\right):\left(x-2\right)=x^2+3x+6\)
c) (-2x5 : 2x2) + (3x2 : 2x2) + (-4x^3 : 2x^2)
= \(-x^3+\dfrac{3}{2}-2x\)
d) \(\left(x^3-64\right):\left(x^2+4x+16\right)\)
\(=\left(x-4\right)\left(x^2+4x+16\right):\left(x^2+4x+16\right)\)
\(=x-4\)
(dùng hẳng đẳng thức thứ 7)
Bài 2 :
a) 3x(x - 2) - 5x(1 - x) - 8(x2 - 3)
= 3x2 - 6x - 5x + 5x2 - 8x2 + 24
= (3x2 + 5x2 - 8x2) + (-6x - 5x) + 24
= -11x + 24
b) (x - y)(x2 + xy + y2) + 2y3
= x3 - y3 + 2y3
= x3 + y3
c) (x - y)2 + (x + y)2 - 2(x - y)(x + y)
= (x - y)2 - 2(x - y)(x + y) + (x + y)2
= [(x - y) + x + y)2 = [x - y + x + y] = (2x)2 = 4x2
Đúng 0
Bình luận (0)
Bài 1 :
a]= \(\frac{1}{4}\)x3 + x - \(\frac{3}{2}\).
b] => [x3 + x2 -12 ] = [ x2 +3 ][x-2] + [-6]
c]= -x3 -2x +\(\frac{3}{2}\).
d] = [ x3 - 64 ] = [ x2 + 4x + 16][ x- 4].
Đạo hàm của hàm số
y
2
x
5
-
4
x
3
-
x
2
là A.
y
5
x
4
-
12
x
2
-
2
x
B.
y
10
x
4
-
12...
Đọc tiếp
Đạo hàm của hàm số y = 2 x 5 - 4 x 3 - x 2 là
A. y ' = 5 x 4 - 12 x 2 - 2 x
B. y ' = 10 x 4 - 12 x 2 - 2 x
C. y ' = 10 x 4 - 3 x 2 - 2 x
D. y ' = 10 x 4 + 12 x 2 - 2 x
Cho hàm số
f
(
x
)
x
4
-
4
x
3
+
2
x
2
-
x
+
1
,∀ x∈ R. Tính
∫
0
1
f
2
(
x
)
.
f
(
x
)
dx
. ...
Đọc tiếp
Cho hàm số f ( x ) = x 4 - 4 x 3 + 2 x 2 - x + 1 ,∀ x∈ R. Tính ∫ 0 1 f 2 ( x ) . f ' ( x ) dx .
A. 2 3
B. 2.
C. - 2 3
D. -2
Cho hàm số
y
3
x
3
+
2
x
2
+
1
. Đạo hàm y của hàm số là: A.
3
x
2
+
2
x
2
3
x
3...
Đọc tiếp
Cho hàm số y = 3 x 3 + 2 x 2 + 1 . Đạo hàm y' của hàm số là:
A. 3 x 2 + 2 x 2 3 x 3 + 2 x 2 + 1
B. 3 x 2 + 2 x + 1 2 3 x 3 + 2 x 2 + 1
C. 9 x 2 + 4 x 3 x 3 + 2 x 2 + 1
D. 9 x 2 + 4 x 2 3 x 3 + 2 x 2 + 1
cho đa thức Q(x)=-3x4+4x3+2x2+2/3-3x-2x4-4x3+8x4+1+3x
Tính đạo hàm của hàm số
y
ln
(
x
4
+
4
x
3
-
3
)
Đọc tiếp
Tính đạo hàm của hàm số y = ln ( x 4 + 4 x 3 - 3 )
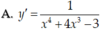
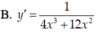
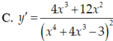
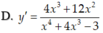
(6x4-4x3+x2+x):(2x2+2x+1)
\((6x^4-4x^3+x^2+x):(2x^2-2x+1)=3x^2+x\)
Đúng 0
Bình luận (0)
(x5 + 4x3 -2x2 + x) : ( x2 - x + 1)
Biết rằng đồ thị của hàm số
y
P
x
x
3
−
2
x
2
−
5
x
+
2
cắt trục hoành tại ba điểm phân biệt lần lượt có hoành độ là
x
1
,
x
2
,
x
3
. Khi đó giá trị của biểu thức
T...
Đọc tiếp
Biết rằng đồ thị của hàm số y = P x = x 3 − 2 x 2 − 5 x + 2 cắt trục hoành tại ba điểm phân biệt lần lượt có hoành độ là x 1 , x 2 , x 3 . Khi đó giá trị của biểu thức T = 1 x 1 2 − 4 x 1 + 3 + 1 x 2 2 − 4 x 2 + 3 + 1 x 3 2 − 4 x 3 + 3 bằng
A. T = 1 2 − P ' 1 P 1 + P ' 3 P 3
B. T = 1 2 − P ' 1 P 1 − P ' 3 P 3
C. T = 1 2 P ' 1 P 1 − P ' 3 P 3
D. T = 1 2 P ' 1 P 1 + P ' 3 P 3
Đáp án C
Ta có: T = 1 x 1 − 1 x 1 − 3 + 1 x 2 − 1 x 2 − 3 + 1 x 3 − 1 x 3 − 3
T = 1 x 1 − 1 x 1 − 3 + 1 x 2 − 1 x 2 − 3 + 1 x 3 − 1 x 3 − 3 vì 1 x − 1 x − 3 = 1 x − 3 − 1 x − 1 .
Vì x 1 , x 2 , x 3 là 3 nghiệm của phương trình P x = 0 ⇒ P x = x − x 1 x − x 2 x − x 3 .
Suy ra P ' x = x − x 1 x − x 2 + x − x 2 x − x 3 + x − x 3 x − x 1
⇒ P ' x P x = x − x 1 x − x 2 + x − x 3 + x − x 3 x − x 1 x − x 1 x − x 2 x − x 3 = 1 x − x 1 + 1 x − x 2 + 1 x − x 3 * .
Thay x = 1 , x = 3 vào biểu thức (*), ta được T = 1 2 P ' x P 1 − P ' 3 P 3 .
Đúng 0
Bình luận (0)