cho tam giác ABC vuông góc tại A;AB =8cm,AC =6cm gọi M là trung điểm AC và E là trung điểm BC.
a,tính EM
b,tứ giác AMEB là hình gì?vì sao?
c,tính chu vi hình thang AMEB?
1) Cho tam giác ABC vuông tại A có góc B = 60độ, AC = 3cm. Tính BC, AB
2) Cho tam giác ABC vuông tại A có BC = 10cm, góc C = 3cm. Tính góc B, AB, AC
3) Cho tam giác ABC vuông tại A có AB = 4cm, góc B = 50 độ. Tính BC, góc C, AC
3:
góc C=90-50=40 độ
Xét ΔABC vuông tại A có sin C=AB/BC
=>4/BC=sin40
=>\(BC\simeq6,22\left(cm\right)\)
\(AC=\sqrt{BC^2-AB^2}\simeq4,76\left(cm\right)\)
1:
góc C=90-60=30 độ
Xét ΔABC vuông tại A có
sin B=AC/BC
=>3/BC=sin60
=>\(BC=\dfrac{3}{sin60}=2\sqrt{3}\left(cm\right)\)
=>\(AB=\dfrac{2\sqrt{3}}{2}=\sqrt{3}\left(cm\right)\)
cho tam giác ABC vuông tại A biết B=40 độ,tính C
2)cho tam giác ABC vuông tại B ,biết góc A=góc 2C,tính góc A,C
+)ΔABC vuông tại A \(\Rightarrow\widehat{A}=90^o\)
+)Áp dụng định lý tổng ba góc trong tam giác vào tam giác ABC, ta có:
\(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)
\(=>90^o+40^o+\widehat{C}=180^o\)
\(=>\widehat{C}=180^o-90^o-40^o=50^o\)
Vậy \(\widehat{C}=50^o\)
------------------------------------------
+)Tam giác ABC vuông tại B \(\Rightarrow\widehat{B}=90^o\)
+)\(\widehat{A}=2.\widehat{C}\Rightarrow\widehat{A}+\widehat{C}=2.\widehat{C}+\widehat{C}=3.\widehat{C}\)
+)Áp dụng định lý tổng ba góc trong tam giác vào tam giác ABC, ta có:
\(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)
\(\Rightarrow\widehat{A}+90^o+\widehat{C}=180^o\)
\(=>\widehat{A}+\widehat{C}=180^o-90^o\)
\(=>3.\widehat{C}=90^o\)
\(=>\widehat{C}=\dfrac{90^o}{3}=30^o\)
+)\(\widehat{A}=2.\widehat{C}\Rightarrow\widehat{A}=2.30^o=60^o\)
Vậy: \(\widehat{A}=60^o\) ; \(\widehat{C}=30^o\)
1: góc C=90-40=50 độ
2: góc A=2/3*90=60 độ
góc C=90-60=30 độ
Cho tam giác ABC vuông tại A có góc B=60 °. Tia phân giác của góc ABCcho tam giác abc vuông tại a có góc b = 60 độ . tia phân giác của góc b cắt ac tại e , kẻ eh vuông góc đc tại h a) chứng minh tam giác abe = tam giác hbe b) hb=hc C) từ H kẻ đường thẳng song song với BE cắt AC ở K .c/m🔺AHK là tam giác đều d) gọi I là giao điểm của BA và HE. Chúng minh IE>EH
a: Xét ΔBAE vuông tại A và ΔBHE vuông tại H có
BE chung
góc ABE=góc HBE
=>ΔBAE=ΔBHE
b: Xét ΔEBC có góc EBC=góc ECB
nên ΔEBC cân tại E
mà EH là đường cao
nên H là trung điểm của BC
=>HB=HC
d: Xét ΔEAI vuông tại A và ΔEHC vuông tại H có
EA=EH
góc AEI=góc HEC
=>ΔEAI=ΔEHC
=>EI=EC>EH
đề 1:
Cho tam giác ABC vuông tại A, AH vuông góc BC,AB=30cm,AH=24cm.
a)tính BH?BC?
b)tính các tỉ số lượng giác của các góc của tam giác AHB
đề 2
cho tam giác ABC vuông tại A, AH vuông góc BC , HB=4cm, HC=9cm
a)tính các cạnh tam giác ABC
b)tính các góc của tam giác ABC
Cho tam giác ABC và vuông góc tại A,Tia phân giác góc B cắt AC tại D a) cho góc ABC = 40 độ.tính Góc ABD b) lấy E thuộc BC: BE=BA.CMR: góc BAD = góc BED và DE vuông góc với BC c) BA cắt ED tại F.CMR: tam giác ABC= tam giác EBF d) vẽ CK vuông góc với BD tại k.CMR: K,F,C thẳng hàng
a , BD là phân giác của \(\widehat{ABC}\)
\(\Rightarrow\) \(\widehat{ABC}=\frac{1}{2}.\widehat{ABC}=\frac{1}{2}.40^o=20^o\)
b , BD là phân giác của \(\widehat{ABC}\) \(\Rightarrow\) \(\widehat{ABD}=\widehat{EBD}\)
Xét ΔABD và ΔEBD có :
BD chung ; \(\widehat{ABD}\) \(=\) \(\widehat{EBD}\); AB = EB ( gt )
\(\Rightarrow\) ΔABD = ΔEBD ( c.g.c )
\(\Rightarrow\) \(\widehat{BAD}\) \(=\) \(BED\) ( đpcm )
\(\Rightarrow\) \(\widehat{BED}=90^o\) \(\Rightarrow\) \(DE\) ⊥ \(BC\) ( đpcm )
c , Xét 2 tam giác vuông : ΔABC và ΔEBF có :
\(\widehat{B}\) chung ; AB = BE ( gt )
\(\Rightarrow\) ΔABC = ΔEBF ( cgv - gn ) ( đpcm )
d , Xét ΔBCF có FE , CA là đường cao , FE ∩ CA tại D
\(\Rightarrow\) D là trực tâm ⇒ BD ⊥ CF
Mà BD ⊥ CK ( gt )
\(\Rightarrow\) C, K, F thẳng hàng ( đpcm )
Bài 1 : Cho xOy có Oz là tia phân giác, M là điểm bất kì thuộc tia Oz. Qua M kẻ đường thẳng a vuông góc với Ox tại a cắt Oy tại C và vẽ đường thẳng b vuông góc với Oy tại B cắt tia Ox tại D. Chứng minh tam giác AOM bằng tam giác BOM ?
Bài 2 : Cho tam giác ABC có góc A = 90* và đường phân giác BH (H thuộc AC). Kẻ HM vuông góc với BC (M thuộc BC). Gọi N là giao điểm của AB và MH. Chứng minh tam giác ABH bằng tam giác MBH, tam giác ACE= tam giác AKE?
Bài 3: Cho tam giác ABC vuông tại C có góc A = 60* và đường phân gác của góc BAC cắt BC tại E. Kẻ EK vuông góc AB tại K (K thuộc AB). Kẻ BD vuông góc với AE tại D (D thuộc AE). Chứng minh tam giác ACE = tam giác AKE
Bài 4: Cho tam giác ABC vuông tại A có đường phân giác của góc ABC cắt AC tại E. Kẻ EH vuông góc BC tại H (H thuộc BC). Chứng minh tam giác ABE = tam giác HBE ?
a)Cho tam giác ABC vuông tại A, biết AB=4cm; BC=5cm, Tonhs cosC+TanB
b) Cho tam giác ABC vuông tại A, có AB=5cm,BC=10cm. Tính sinC và số đo góc B
c) Cho tam giác ABC vuông tại A, biết cosB=8cm. hãy tính các tỉ số lượng giác của góc C. E c.ơn ạ!
Câu a) với b) tính cos, tan, sin là tính góc hay cạnh vậy cậu?
a) Xét \(\Delta ABC\) vuông tại `A`
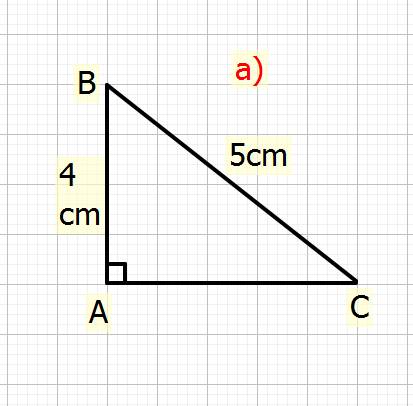
Ta có: \(BC^2=AB^2+AC^2\) (đl Pytago)
\(\Rightarrow5^2=4^2+AC^2\\ \Rightarrow AC^2=5^2-4^2\\ \Rightarrow AC^2=25-16=9\\ \Rightarrow AC=\sqrt{9}=3cm\)
Vậy: \(AC=3cm\)
Ta có: \(CosC=\dfrac{AC}{BC}\left(tslg\right)\)
\(\Rightarrow CosC=\dfrac{3}{5}\\ \Rightarrow CosC\approx53^o\)
Vậy: Góc C khoảng \(53^o\)
Ta có: \(TanB=\dfrac{AC}{AB}\left(tslg\right)\)
\(\Rightarrow TanB=\dfrac{3}{4}\\ \Rightarrow TanB\approx37^o\)
Vậy: Góc B khoảng \(37^o\)
_
b) Xét \(\Delta ABC\) vuông tại `A`
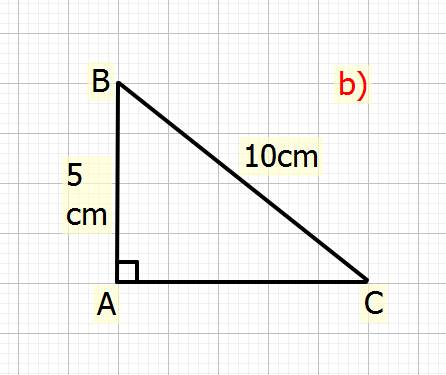
Ta có: \(BC^2=AB^2+AC^2\) (đl Pytago)
\(\Rightarrow10^2=5^2+AC^2\\ \Rightarrow AC^2=10^2-5^2\\\Rightarrow AC^2=100-25=75\\ \Rightarrow AC=\sqrt{75}=5\sqrt{3}cm\)
Vậy: \(AC=5\sqrt{3}cm\)
Ta có: \(SinC=\dfrac{AB}{BC}\left(tslg\right)\)
\(\Rightarrow SinC=\dfrac{5}{10}\\ \Rightarrow30^o\)
Vậy: Góc C là \(30^o\)
Ta có: \(SinB=\dfrac{AC}{BC}\left(tslg\right)\)
\(\Rightarrow SinB=\dfrac{5\sqrt{3}}{10}\\ \Rightarrow SinB=60^o\)
Vậy: Góc B là \(60^o\).
Cho tam giác ABC có góc A nhọn. Về phía ngoài của tam giác ABC vẽ tam giác BAD vuông cân tại A, tam giác CAE vuông cân tại A. CM:
a) DC = BE; DC vuông góc với BE
b) BD2 + CE2 = BC2 + DE2
c) Đường thẳng qua A vuông góc với DE cắt BC tại K. Chứng minh K là trung điểm của BC\
HELP ME
1. Cho tam giác ABC cân tại A có góc A = 20 độ. Vẽ D trên nửa mặt phẳng bờ AC không chứa B sao cho tam giác BCD cân tại C và góc BCD = 140 độ. Tính góc ADC
2. Cho tam giác ABC cân tại A có góc BAC = 108 độ. D là điểm nằm trong tam giác ABC sao cho góc DBC = 12 độ, góc DCB = 18 độ. tính góc ADB
3. Cho tam giác ABC cân tại A, A = 100 độ. M nằm trong tam giác ABC sao cho góc MBC = 30 độ, góc MCB = 20 độ. Tính góc MAC
4. Cho tam giác ABC vuông tại A, vẽ AH vuông góc vs BC tại. Biết BH - HC = AC. tính các góc ABC, ACB
Cho tam giác ABC vuông tại A có góc B bằng 30° và tam giác MNP vuông tại góc M có góc P bằng 60°. Chứng minh tam giác ABC đồng dạng với tam giác MNP.
Ta có: <A+<B+<C=180
90+30+<C=180
<c=180-30-90=60
Xét ▲ABC và ▲MNP ta có:
<A=<M=90
<C=<P(=60)
Do đó ▲ABC đồng dạng ▲MNP(g-g)