Rút gọn biểu thức :
M = \(\frac{a}{ab+a+2}+\frac{b}{bc+b+1}+\frac{c}{ac+2c+2}\) Biết : abc =2
Rút gọn biểu thức : M = \(\frac{a}{ab+a+2}+\frac{b}{bc+b+1}+\frac{c}{ac+2c+2}\) Biết abc = 2
thế abc=2 vào M ta có
M=\(\frac{a}{ab+b+abc}\)+ \(\frac{b}{bc+b+1}\)+ \(\frac{abc^2}{ac+abc^2+abc}\)
M=\(\frac{a}{a\left(bc+b+1\right)}\)+\(\frac{b}{bc+b+1}\)+ \(\frac{abc^2}{ac\left(bc+b+1\right)}\)
M=\(\frac{bc+b+1}{bc+b+1}\)=1
1 nha bạn cho mình nha
Cho abc = 2. Rút gọn biểu thức M= \(\frac{a}{ab+a+2}+\frac{b}{bc+b+1}+\frac{c}{ac+2c+2}\)
Ta có ; \(\frac{a}{ab+a+2}\)+\(\frac{b}{bc+b+1}\)+\(\frac{c}{ac+2c+2}\)
=\(\frac{a}{ab+a+2}\)+\(\frac{ab}{abc+ab+a}\)+\(\frac{c}{ac+2c+abc}\)
=\(\frac{a}{ab+a+2}\)+\(\frac{ab}{a+ab+2}\)+\(\frac{c}{c\left(a+2+ab\right)}\)
=\(\frac{a}{ab+a+2}\)+\(\frac{ab}{a+ab+2}\)+\(\frac{1}{a+ab+2}\)
=\(\frac{a+ab+1}{ab+a+2}\)
Đề bài này hình như có gì sai bạn ạ
đáng ra phải là \(\frac{2c}{ac+2c+2}\) chứ
Đề đúng là \(\frac{a}{ab+a+2}+\frac{b}{bc+b+1}+\frac{2c}{ac+2c+2}\)
Đây là toán violympic nên có vài mẹo nhỏ để làm nhanh hơn nhé!
Đối với bài này, có abc=2, ta có thể cho a=1,b=1,c=2.
Thay số vào \(M=\frac{1}{1+1+2}+\frac{1}{2+1+1}+\frac{4}{2+4+2}\)= \(\frac{1}{4}+\frac{1}{4}+\frac{1}{2}=1\)
(Bạn có thể thử kết quả với các số a,b,c khác)
Cho \(abc=2\). Rút gọn biểu thức :
\(M=\frac{a}{ab+a+2}+\frac{b}{bc+b+1}+\frac{2c}{ac+2c+2}\)
Help me please!
Mai mình phải nộp rồi!
Vì \(abc=2\)nên ta có:
\(M=\frac{a}{ab+a+2}+\frac{b}{bc+b+1}+\frac{2c}{ac+2c+2}\)
\(=\frac{a}{ab+a+abc}+\frac{b}{bc+b+1}+\frac{abc.c}{ac+abc.c+abc}\)
\(=\frac{a}{a\left(b+1+bc\right)}+\frac{b}{bc+b+1}+\frac{abc^2}{ac\left(1+bc+b\right)}\)
\(=\frac{1}{bc+b+1}+\frac{b}{bc+b+1}+\frac{bc}{bc+c+1}\)
\(=\frac{1+b+bc}{bc+c+1}=1\)
câu trả lời;
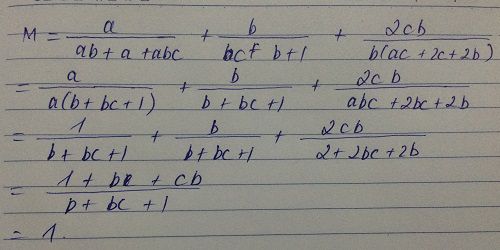
\(M=\frac{a}{ab+a+2}+\frac{b}{bc+b+1}+\frac{2c}{ac+2c+2}\)
\(M=\frac{a}{ab+a+abc}+\frac{b}{bc+b+1}+\frac{abc.c}{ac+abc.c+abc}\)
\(M=\frac{1}{b+1+bc}+\frac{b}{bc+b+1}+\frac{bc}{1+bc+b}=1\)
Cho abc = 2 .Rút gọn biểu thức :
\(M=\frac{a}{ab+a+2}+\frac{b}{bc+b+1}+\frac{2c}{ac+2c+2}\)
\(M=\frac{a}{ab+a+abc}+\frac{b}{bc+b+1}+\frac{2c}{abc+2bc+2b}\)
\(=\frac{a}{a\left(b+1+bc\right)}+\frac{b}{bc+b+1}+\frac{2bc}{2+2bc+2b}\)
\(=\frac{1}{b+1+bc}+\frac{b}{bc+b+1}+\frac{2bc}{2\left(1+bc+b\right)}\)
\(=\frac{1}{b+1+bc}+\frac{b}{bc+b+1}+\frac{2bc}{2\left(1+bc+b\right)}\)
\(=\frac{1+b+bc}{b+1+bc}=1\)
Vậy \(M=1.\)
Cho \(abc=2\)
Rút gọn biểu thức :
\(A=\frac{a}{ab+a+2}+\frac{b}{bc+b+1}+\frac{2c}{ac+2c+2}\)
Học sinh tiểu học làm được đấy
๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ ๑๑۩۞۩๑๑ v
Bài này chịu mất.Cần có nhiều thời gian suy nghĩ
Rút gọn biểu thức:
M= a/(ab+a+2)+b/(bc+b+1)+c/(ac+2c+2). Biết abc=2
Cho abc =2 . Rút gọn biểu thức :
M=\(\frac{a}{ab+a+2}\)+\(\frac{b}{bc+b+1}\)+\(\frac{2c}{ac+2c+2}\).Ta được kết quả M = ?
\(\frac{a}{ab+a+2}+\frac{b}{bc+b+1}+\frac{2c}{ac+2c+2}\)
\(=\frac{a}{ab+a+abc}+\frac{b}{bc+b+1}+\frac{2c}{ac+2c+abc}\)
\(=\frac{a}{a\left(b+1+bc\right)}+\frac{b}{b+1+bc}+\frac{2c}{c\left(a+ab+2\right)}\)
\(=\frac{1}{b+bc+1}+\frac{b}{b+bc+1}+\frac{2}{a+2+ab}\)
\(=\frac{1}{b+bc+1}+\frac{b}{b+bc+1}+\frac{bc}{b+bc+1}\)
\(=\frac{b+bc+1}{b+bc+1}=1\)
Theo bài ra , ta có :
\(M=\frac{a}{ab+a+2}+\frac{b}{bc+b+1}+\frac{2c}{ac+2c+2}\)
\(\Leftrightarrow\frac{a}{ab+a+abc}+\frac{b}{bc+b+1}+\frac{2bc}{b\left(ac+2c+2\right)}\)(Vì abc = 2 )
\(\Leftrightarrow\frac{a}{a\left(b+1+bc\right)}+\frac{b}{bc+b+1}+\frac{2bc}{abc+2bc+2b}\)
\(\Leftrightarrow\frac{1}{b+1+bc}+\frac{b}{bc+b+1}+\frac{2bc}{2+2bc+2b}\)( Vì abc = 2 )
\(\Leftrightarrow\frac{1}{b+1+bc}+\frac{b}{bc+b+1}+\frac{2bc}{2\left(1+bc+b\right)}\)
\(\Leftrightarrow\frac{1}{b+1+bc}+\frac{b}{bc+b+1}+\frac{bc}{1+bc+b}\)
\(\Leftrightarrow\frac{1+b+bc}{b+1+bc}=1\)
Vậy M=1
Chúc bạn học tốt =))![]()
Phan Cả Phát xin hết !!!
Giúp mk cho nhanh cái mk đang cần gấp ! cảm ơn nhìu![]()
cho \(abc=2\)
rút gọn: A=\(\frac{a}{ab+a+2}+\frac{b}{bc+b+1}+\frac{c}{ac+2c+2}\)
cho mình xửa lại một chút nha:tính : A=\(\frac{a}{ab+a+2}+\frac{b}{bc+b+1}+\frac{2c}{ca+2c+2}\)
Cho abc=2. Rút gọn biểu thức: \(M=\dfrac{a}{ab+a+2}+\dfrac{b}{bc+b+1}+\dfrac{2c}{ac+2c+2}\)
M\(=\dfrac{a}{ab+a+2}+\dfrac{b}{bc+b+1}+\dfrac{2c}{ac+2c+2}\)
\(M=\dfrac{a}{ab+a+abc}+\dfrac{b}{bc+b+1}+\dfrac{2bc}{b\left(ac+2c+2\right)}\)
M = \(\dfrac{a}{a\left(b+1+bc\right)}+\dfrac{b}{b+1+bc}+\dfrac{2bc}{abc+2bc+2b}\)
M=\(\dfrac{1}{b+1+bc}+\dfrac{b}{b+1+bc}+\dfrac{2bc}{2+2bc+2b}\)
M = \(\dfrac{1+b}{b+1+bc}+\dfrac{2bc}{2\left(1+bc+b\right)}\)
M = \(\dfrac{1+b}{b+1+bc}+\dfrac{bc}{b+1+bc}=\dfrac{1+b+bc}{b+1+bc}=1\)