có 5 quả bi vàng, 6 quả bi xanh, 4 quả bi đỏ
chọn 4 quả bi. Tính xác suất để 4 quả bi có đủ 3 màu
Nam lấy ra ngẫu nhiên một viên bi từ trong hộp có chứa 4 viên bi xanh, 3 viên bi đỏ, 3 viên bi vàng. a. Liệt kê tất cả các kết quả có thể xảy ra đối với màu của viên bi b. Nêu 2 điều cần chú ý trong mô hình xác suất của trò chơi trên c. Có bao nhiêu kết quả có thể xảy ra khi viên bi lấy ra phải có màu xanh (không tính sự trùng lặp màu của viên bi được lấy ra trong các lần) d. Tính xác suất lấy được viên bi màu xanh
1) Có 5 quả bóng đỏ,5 quả bóng trắng và 5 quả bóng vàng trong 1 chiếc túi.Hỏi phải lấy ít nhất bao nhiêu quả bóng để chắc chắn có được 3 quả khác màu?
2) Trong 1 chiếc túi có 4 viên bi đỏ,7 viên bi xanh lá cây,6 viên bi xanh da trời,2 viên bi màu da cam.Hỏi nếu bị bịt mắt An phải lấy ra ít nhất bao nhiêu viên bi để chắc chắn có 4 viên bi khác màu nhau?
Trả lời nhanh lên nhé mai mình phải nộp rồi,ghi cả cách giải cụ thể nhé.Ai nhanh mình tích cho
1 ) Phải lấy ít nhất số quả bóng để chắc chắn có được 3 quả khác màu là :
5 + 5 + 1 = 11 ( quả )
Đáp số : 11 quả bóng
2 ) Nếu bị bịt mắt , An phải lấy ra ít nhất số viên bi để chắc chắn có 4 viên khác màu là :
7 + 6 + 4 + 1 = 18 ( viên )
Đáp số : 18 viên bi
Nam lấy ra một viên bi từ trong hộp có chứa 4 viên bi xanh, 3 viên bi đỏ , 3 viên bi vàng.
a) Liệt kê tất cả kết quả có thể
b) Sự kiện"Nam lấy được viên bi xanh" có luôn xảy ra không?
c) Tính xác suất lấy được viên bi màu xanh.
ét ô ét giúp tui nha
a. Có 3 kết quả có thể xảy ra
b. Sự kiện đó không thể luôn xảy ra
c. Xác suất thực nghiệm lấy được bi màu xanh là: \(\dfrac{4}{4+3+3}=0,4=40\%\)
Có 3 kết quả có thể xảy ra đối với màu của viên bi đc lấy ra, đó là:
Sự kiện “Nam lấy được viên bi xanh” không luôn xảy ra.
Xác suất lấy được viên bi màu xanh là:
Trong một túi có 3 quả bi xanh, 7 quả bi vàng, 18 quả bi trắng và 23 quả bi đen. Hỏi phải bốc ít nhất bao nhiêu quả (không nhìn) để ta có chắc chắn 9 quả bi cùng màu?
tổng các số bị sẽ là:
3+7+18+23=51(viên)
không nhìn ta sẽ lấy tất cả số viên là:
1+4+11+5=21(viên)
giải thích:3 viên là lấy 1 ,7 viên là lấy 4,18 viên là lấy 11,23 viên là lấy 5
ta sẽ chắc chắn lấy tất cả số viên là:
51-21=30 viên
đáp số:30 viên
Gieo hai hột xúc sắc xanh và đỏ. Gọi x, y là kết quả số nút của hai hột xúc sắc đó. Có 2 bình, bình 1 đựng 6 bi xanh và 4 bi vàng, bình 2 đựng 3 bi xanh và 6 bi vàng. Nếu ![]() thì bốc ra 2 bi từ bình 1, còn nếu
thì bốc ra 2 bi từ bình 1, còn nếu ![]() thì bốc ra 2 bi từ bình 2. Tính xác suất để bốc được ít nhất một bi xanh.
thì bốc ra 2 bi từ bình 2. Tính xác suất để bốc được ít nhất một bi xanh.
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Đáp án D
Kết quả gieo hai hột súc sắc đỏ thì không gian mẫu có 36 cặp ![]() trong đó chỉ có 6 cặp
trong đó chỉ có 6 cặp ![]() có tổng nhỏ hơn 5. Đó là
có tổng nhỏ hơn 5. Đó là ![]()
![]()
Bình 1 đựng 6 bi xanh và 4 bi vàng
=> xác suất bốc cả 2 bi vàng từ bình là ![]()
Bình 2 đựng 3 bi xanh và 6 bi vàng
=> xác suất bốc được ít nhất 1 bi xanh từ bình 2 là 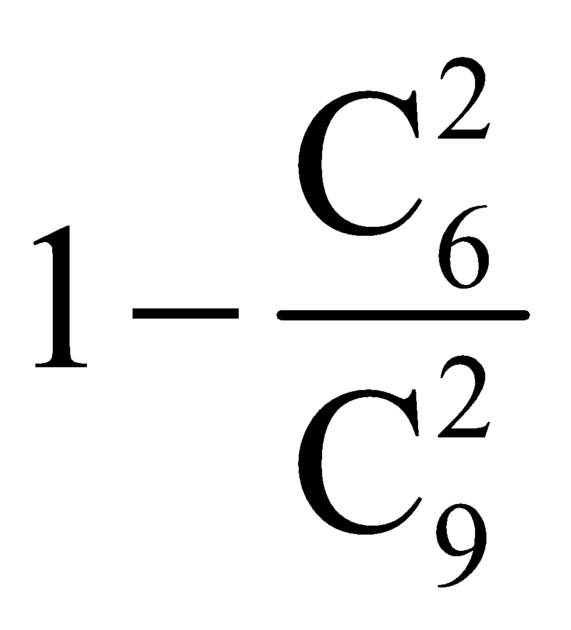
Do đó xác suất để bốc được ít nhất 1 bi xanh trong trò chơi là 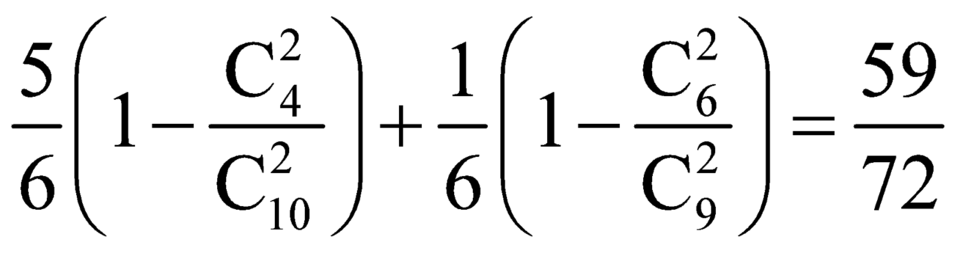
Gieo hai hột xúc sắc xanh và đỏ. Gọi x, y là kết quả số nút của hai hột xúc sắc đó. Có 2 bình, bình 1 đựng 6 bi xanh và 4 bi vàng, bình 2 đựng 3 bi xanh và 6 bi vàng. Nếu x + y ≥ 5 thì bốc ra 2 bi từ bình 1, còn nếu x+y < 5 thì bốc ra 2 bi từ bình 2. Tính xác suất để bốc được ít nhất một bi xanh.
A. 29/36
B. 5/6
C. 13/72
D. 59/72
Một hộp có 4 bi đỏ, 6 bi xanh và 5 bi vàng. Ngta chọn 4 viên bi từ hộp đó. Hỏi tính xác suất có bao nhiêu cách chọn để có 4 viên bi lấy ra ko có đủ cả 3 màu .
Không gian mẫu là 15C4 = 1365.
Lấy từ hộp 4 viên có đủ 3 màu.
4C2.5C1.6C1 + 4C1.5C2.6C1 + 4C1.5C1.6C2 = 720
=> P = 1 - 720/1365
2. Trong một túi có 3 quả bi xanh, 7 quả bi vàng, 18 quả bi trắng và 23 quả bi đen. Häi phải bốc ít nhấtt bao nhiêu quả (không nhìn) để ta có chắc chắn 9 quả bi cùng màu?
Từ một hộp đựng 8 bi xanh, 9 bi đỏ, 10 bi vàng, chọn ra 4 bi
Tính xác suất để 4 bi chọn thõa:
a. Có đúng 2 bi đỏ
b. Có đủ 3 màu
c. Không có đủ 3 màu
Không gian mẫu: \(C_{27}^4\)
a. Số cách chọn ra 2 bi đỏ: \(C_9^2.C_{18}^2\)
Xác suất: \(P_1=\dfrac{C_9^2.C_{18}^2}{C_{27}^4}=...\)
b. Số cách chọn ra 4 bi có đúng 1 màu: \(C_8^4+C_9^4+C_{10}^4\)
Số cách chọn ra 4 bi có đúng 2 màu: \(C_{17}^4+C_{18}^4+C_{19}^4-2\left(C_8^4+C_9^4+C_{10}^4\right)\)
Số cách chọn ra 4 bi có đủ 3 màu:
\(C_{27}^4-\left(C_{17}^4+C_{18}^4+C_{19}^4-2\left(C_8^4+C_9^4+C_{10}^4\right)+C_8^4+C_9^4+C_{10}^4\right)\)
Xác suất: \(P_2=\dfrac{C_{27}^4-\left(C_{17}^4+C_{18}^4+C_{19}^4-\left(C_8^4+C_9^4+C_{10}^4\right)\right)}{C_{27}^4}=...\)
c. Xác suất: \(P_3=1-P_2=...\)