Có a<b (1) và b<c (2)

Cộng vế theo vế của (1) và (2) ta được : a+b<b+c

=> a<c ( trừ 2 vế với b)

Nếu a<b và b<c

=> a + b < b + c

Hay a < c ( ĐPCM )

a) Vì số nguyên âm luôn bé hơn 0 mà số nguyên dương lại lớn hơn 0

\(\Rightarrow\) Một số nguyên âm bao giờ cũng nhỏ hơn một số nguyên dương bất kì.

b) Vì số nguyên a lớn hơn 2 mà 2 > 0

=> a là số nguyên dương

c) Vì số nguyên a nhỏ hơn -1 mà -1 < 0

=> a là số nguyên âm

Hướng dẫn:

a) a là số nguyên âm, b là số nguyên dương: a < 0 , 0 < b ⇒ a < b .

b) a > 2 , 2 > 0 ⇒ a > 0 ;

c) a < -1 , -1 < 0 ⇒ a < 0 .

Theo đề bài ta có 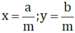 (a, b, m ∈ Z; m > 0).

Quy đồng mẫu số các phân số ta được: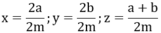 

Nhận xét: mẫu số 2m > 0 nên để so sánh x, y, z ta so sánh các tử số 2a, 2b, a+b.

   Vì a < b nên a + a < b + a hay 2a < a + b.

   Vì a < b nên a + b < b + b hay a + b < 2b.

Vậy ta có 2a < a+b < 2b nên 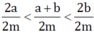 hay x < z < y.

Vì x < y (a/m < b/m) và m > 0 nên a < b . 

x = a / m = 2a / 2m ; y = b / m = 2b / 2m ; z = a + b / 2m

a < b => a + a < a + b < b + b <=> 2a < a + b < 2b => 2a / 2m < a + b / 2m < 2b / 2m => x < z < y

ta có x=a/m = 2a/2m ; y= b/m= 2b/2m ; z= (a+b)/2m
lại có x<y <=> a<b (do m>0)
<=> a+a < a+b < b + b 
<=> 2a < a+b < 2b 
<=> 2a/2m <(a+b)/2m <2b/2m
<=> x<z<y

 x =a/m =>. x = 2a/2m 
y =b/m => y = 2b/2m 
z = (a+b)/2m 
theo giả thiết a < b => a + b < b + b => a + b < 2b ........(1) 
Ngòa i ra, a < b => a + a < a + b => 2a < a + b ........(2) 
Suy ra: 
2a < a +b < 2b 
Suy ra (chia 2 vế cho 2m) : 
2a/2m < (a +b)/2m < 2b 
R út gọn ta được : x < z <y

cái này mk chịu thôi

`a vdots m,b vdots m`

`=>a+b vdots m`

Mà `a+b+c vdots m`

`=>a+b+c-(a+b) vdots m`

`=>a+b+c-a-b vdots m`

`=>(a-a)+(b-b)+c vdots m`

`=>0+0+c vdots m`

`=>c vdots m(forall a,b,c in Z)`