Trong không gian Oxyz cho một vecto a → tùy ý khác vecto 0 → . Gọi α , β , γ là ba góc tạo bởi ba vecto đơn vị i → , j → , k → trên ba trục Ox, Oy, Oz và vecto a → . Chứng minh rằng: cos 2 α + cos 2 β + cos 2 γ = 1
PB
Những câu hỏi liên quan
Trong không gian cho ba vecto tùy ý
a
→
,
b
→
,
c
→
Gọi
u
→
a
→
− 2
b
→
,
v
→
3
b
→
−
c...
Đọc tiếp
Trong không gian cho ba vecto tùy ý a → , b → , c →
Gọi u → = a → − 2 b → , v → = 3 b → − c → , w → = 2 c → − 3 a →
Chứng tỏ rằng ba vecto u → , v → , w → đồng phẳng.
Muốn chứng tỏ rằng ba vecto u → , v → , w → đồng phẳng ta cần tìm hai số thực p và q sao cho w → = p u → + q v →
Giả sử có w → = p u → + q v →
2 c → – 3 a → = p( a → – 2 b → ) + q(3 b → − c → )
⇔ (3 + p) a → + (3q − 2p) b → − (q + 2) c → = 0 → (1)
Vì ba vecto lấy tùy ý a → , b → , c → nên đẳng thức (1) xảy ra khi và chỉ khi:
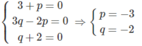
Như vậy ta có: w → = −3 u → − 2 v → nên ba vecto u → , v → , w → đồng phẳng.
Đúng 0
Bình luận (0)
Trong không gian Oxyz, cho mặt phẳng
P
:
x
−
3
z
+
2
0.
Vecto nào sau đây là một vecto pháp tuyến của (P)? A.
w
→
1
;
0
;
−
3
B.
v
→
2...
Đọc tiếp
Trong không gian Oxyz, cho mặt phẳng P : x − 3 z + 2 = 0. Vecto nào sau đây là một vecto pháp tuyến của (P)?
A. w → = 1 ; 0 ; − 3
B. v → = 2 ; − 6 ; 4
C. u → = 1 ; − 3 ; 0
D. n → = 1 ; − 3 ; 2
Đáp án A.
Phương pháp
Cho mặt phẳng P : a x + b y + c z + d = 0 thì VTPT của (P) là: n → = a ; b ; c
Cách giải
Theo đề bài ta thấy VTPT của (P): n → = 1 ; 0 ; − 3
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): 2x+y+2=0. Vecto nào dưới đây là một vecto pháp tuyến của (P)
A. (2;0;1)
B. (2;1;0)
C. (2;1;2)
D. (2;-1;0)
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): 2x-2z+z+2017=0. Vecto nào dưới đây là một vecto pháp tuyến của (P)
A. (1;-1;4)
B. (1;-2;2)
C. (2;2;1)
D. (-2;2;-1)
Cho ∆ABC với vecto MB= –2 vecto MA, vecto NA+ vecto NC= vecto 0. Gọi k là trung điểm MN.
a) Chứng minh 2vecto AB + 3vecto AC= 12 vecto AK.
b) Với P là điểm tùy ý, gọi Q là điểm thỏa vecto PQ= vecto PA +2vecto PB + vecto PC. Chứng minh đường thẳng PQ luôn đi qua điểm cố định.
🆘🆘🆘GIẢI GIÚP MÌNH VỚI 🆘🆘🆘
Cho ∆ABC với vecto MB= –2 vecto MA, vecto NA+ vecto NC= vecto 0. Gọi k là trung điểm MN.
a) Chứng minh 2vecto AB + 3vecto AC= 12 vecto AK.
b) Với P là điểm tùy ý, gọi Q là điểm thỏa vecto PQ= vecto PA +2vecto PB + vecto PC. Chứng minh đường thẳng PQ luôn đi qua điểm cố định.
Trong không gian Oxyz, cho một vecto pháp tuyến của mặt phẳng ( α ) : 2x - 3z + 1 = 0 là
A. (2;-3;1)
B. (2;0;-3)
C. (0;2;-3)
D. (2;-3;0)
Trong không gian với hệ tọa độ Oxyz, vecto nào cho dưới đây là vecto chỉ phương của mặt phẳng 2x-y-z0? A.
u
→
1
;
-
2
;
1
B.
u
→
1
;
1
;
2
C.
u
→...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, vecto nào cho dưới đây là vecto chỉ phương của mặt phẳng 2x-y-z=0?
A. u → 1 ; - 2 ; 1
B. u → 1 ; 1 ; 2
C. u → 2 ; - 1 ; - 1
D. u → 1 ; 1 ; 1
Trong không gian Oxyz, cho mặt phẳng (P) x + 2y + 4 0. Một vecto pháp tuyến của (P) là A.
n
4
→
1
;
2
;
0
B.
n
2
→
1
;...
Đọc tiếp
Trong không gian Oxyz, cho mặt phẳng (P) x + 2y + 4 = 0. Một vecto pháp tuyến của (P) là
A. n 4 → = 1 ; 2 ; 0
B. n 2 → = 1 ; 4 ; 2
C. n 1 → = 1 ; 0 ; 2
D. n 3 → = 1 ; 2 ; 4


