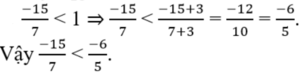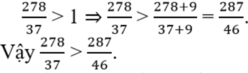So sánh các số hữu tỉ sau: - 157 623 v à - 47 213
PB
Những câu hỏi liên quan
So sánh các số hữu tỉ sau: - 15 7 v à - 6 5
So sánh các số hữu tỉ sau: 278 37 v à 287 46
So sánh các số hữu tỉ sau: 4 9 v à 13 18
4 9 < 1 ⇒ 4 9 < 4 + 9 9 + 9 = 13 18
Vậy 4 9 < 13 18
Đúng 0
Bình luận (0)
so sánh số hữu tỉ sau bằng cách nhanh nhất :
-12/19 và -14/17
Viết số hữu tỉ - 7/20 dưới các dạng sau đây:
a, Tích của 2 số hữu tỉ
b, Thương của 2 số hữu tỉ
c, Tổng của 1 số hữu tỉ dương và 1 số hữu tỉ âm
d, Tổng của 2 số hữu tỉ âm trong đó 1 số là - 1/5
a, Tích của 2 số hữu tỉ
\(\frac{7}{20}\cdot\left(-1\right)=-\frac{7}{20}\)
b, Thương của 2 số hữu tỉ
\(1:-\frac{20}{7}=1\cdot-\frac{7}{20}=-\frac{7}{20}\)
c, Tổng của 1 số hữu tỉ dương và 1 số hữu tỉ âm
\(\frac{3}{5}+\frac{-19}{20}=\frac{12}{20}+\frac{-19}{20}=-\frac{7}{20}\)
d, Tổng của 2 số hữu tỉ âm trong đó 1 số là - 1/5
\(-\frac{1}{5}+\frac{-3}{20}=\frac{-4}{20}+\frac{-3}{20}=-\frac{7}{20}\)
Đúng 0
Bình luận (0)
So sánh số hữu tỉ : -1/25 và 1/1225
Giúp mình câu : Trong các số hữu tỉ sau , số nào là số hữu tỉ dương , số nào là số hữu tỉ âm , số nào kh phải là số hữu tỉ dương mà cũng không phải là số hữu tỉ âm ?
-3 phần 7 , 2 phần 3 , 1 phần -5 , -4 , 0 phần -2 , -3 phần -5 .
Giúp mình với
Số hữu tỉ dương: \(\frac{-3}{-5};\frac{2}{3}\)
Số hữu tỉ âm: \(\frac{-3}{7};\frac{1}{-5}\)
Số không phải là số hữu tỉ âm mà cũng không phải là số hữu tỉ âm: \(\frac{0}{-2}\)
Đúng 0
Bình luận (1)
so sánh hai số hữu tỉ sau bằng cách nhanh nhất
-17/35 và -43/85
Xét xem các số a và b có thể là số vô tỉ hay ko nếu :
a) ab và a/b là các số hữu tỉ
b) a + b và a/b là các số hữu tỉ (a + b khác 0)
c) a + b và a^2 b^2 là các số hữu tỉ ( a + b khác 0)
Ai làm đc mình cho 3 like
Cho 3 **** kiểu gì nào?
a) a,b có thể là số vô tỉ. Ví dụ \(a=b=\sqrt{2}\) là vô tỉ mà ab và a/b đều hữu tỉ.
b) Trong trường hợp này \(a,b\) không là số vô tỉ (tức cả a,b đều là số hữu tỉ). Thực vậy theo giả thiết \(a=bt\), với \(t\) là số hữu tỉ khác \(-1\). Khi đó \(a+b=b\left(1+t\right)=s\) là số hữu tỉ, suy ra \(b=\frac{s}{1+t}\) là số hữu tỉ. Vì vậy \(a=bt\) cũng hữu tỉ.
c) Trong trường hợp này \(a,b\) có thể kaf số vô tỉ. Ví dụ ta lấy \(a=1-\sqrt{3},b=3+\sqrt{3}\to a,b\) vô tỉ nhưng \(a+b=4\) là số hữu tỉ và \(a^2b^2=\left(ab\right)^2=12\) cũng là số hữu tỉ.
Đúng 0
Bình luận (0)