Cho mặt cầu (S) tâm O và các điểm A, B, C nằm trên mặt cầu (S) sao cho A B = 3 , A C = 4 , B C = 5 và khoảng cách từ O đến mặt phẳng (ABC) bằng 1. Thể tích của khối cầu (S) bằng
A. 7 21 π 2
B. 13 13 π 6
C. 20 5 π 3
D. 29 29 π 6
PB
Những câu hỏi liên quan
Cho mặt cầu (S) tâm O và các điểm A, B, C nằm trên mặt cầu (S) sao cho AB3, AC4, BC5 và khoảng cách từ O đến mặt phẳng (ABC) bằng 1. Thể tích của khối cầu (S) bằng
Đọc tiếp
Cho mặt cầu (S) tâm O và các điểm A, B, C nằm trên mặt cầu (S) sao cho AB=3, AC=4, BC=5 và khoảng cách từ O đến mặt phẳng (ABC) bằng 1. Thể tích của khối cầu (S) bằng
Cho mặt cầu (S) tâm O và các điểm A, B, C nằm trên mặt cầu (S) sao cho AB AC 6, BC 8. Khoảng cách từ O đến mặt phẳng (ABC) bằng 2. Thể tích khối cầu (S) bằng A.
404
π
5
B.
2916
π
5
75
.
C.
404
π...
Đọc tiếp
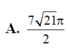
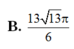
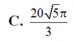
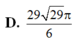
Cho mặt cầu (S) tâm O và các điểm A, B, C nằm trên mặt cầu (S) sao cho AB = AC = 6, BC = 8. Khoảng cách từ O đến mặt phẳng (ABC) bằng 2. Thể tích khối cầu (S) bằng
A. 404 π 5
B. 2916 π 5 75 .
C. 404 π 505 75
D. 324 π 5
Cho 3 điểm A, B, C nằm trên mặt cầu (S) tâm O, AB = 5a, AC = 4a, BC = 3a, khoảng cách từ O đến mặt phẳng (ABC) bằng 2a. Tính thể tích mặt cầu (S) theo a ?
Cho A là điểm nằm trên mặt cầu (S) tâm (O), có bán kính R6cm. I, K là 2 điểm trên đoạn OA sao cho OIIKKA. Các mặt phẳng (α), (b) lần lượt qua I, K cùng vuông góc với OA và cắt mặt cầu (S) theo các đường tròn có bán kính
r
1
,
r
2
. Tính tỉ số
r
1
r
2
A.
r
1...
Đọc tiếp
Cho A là điểm nằm trên mặt cầu (S) tâm (O), có bán kính R=6cm. I, K là 2 điểm trên đoạn OA sao cho OI=IK=KA. Các mặt phẳng (α), (b) lần lượt qua I, K cùng vuông góc với OA và cắt mặt cầu (S) theo các đường tròn có bán kính r 1 , r 2 . Tính tỉ số r 1 r 2
A. r 1 r 2 = 4 10
B. r 1 r 2 = 5 3 10
C. r 1 r 2 = 3 10 4
D. r 1 r 2 = 3 10 5
Cho ba điểm A(3;1;1), B(0;1;4), C(-1;-3;1). Viết phương trình mặt cầu (S) đi qua A, B, C và có tâm nằm trên mặt phẳng (P): x+y-2z+40
Đọc tiếp
Cho ba điểm A(3;1;1), B(0;1;4), C(-1;-3;1). Viết phương trình mặt cầu (S) đi qua A, B, C và có tâm nằm trên mặt phẳng (P): x+y-2z+4=0
Cho ba điểm A(3;1;1), B(0;1;4), C(-1;-3;1). Viết phương trình mặt cầu (S) đi qua A, B, C và có tâm nằm trên mặt phẳng (P):x+y-2z+40 A.
x
+
1
2
+
y
-
1
2
+
z
+
2
2...
Đọc tiếp
Cho ba điểm A(3;1;1), B(0;1;4), C(-1;-3;1). Viết phương trình mặt cầu (S) đi qua A, B, C và có tâm nằm trên mặt phẳng (P):x+y-2z+4=0
A. x + 1 2 + y - 1 2 + z + 2 2 = 9
B. x - 1 2 + y + 1 2 + z - 2 2 = 3
C. x - 1 2 + y + 1 2 + z - 2 2 = 9
D. x + 1 2 + y - 1 2 + z + 2 2 = 3
Chọn C
Gọi tâm mặt cầu I(x;-x+2z-4;z). Tìm x,z từ hệ hai phương trình IA=IB=IC
Đúng 0
Bình luận (0)
Trong không gian Oxyz, cho điểm A(1;0;-1), mặt phẳng (P): x + y - z - 3 0. Mặt cầu (S) có tâm I nằm trên mặt phẳng (P), đi qua điểm A và gốc tọa độ O sao cho chu vi tam giác OIA bằng 6 + √2. Phương trình mặt cầu (S) là: A. (x + 2)2 + (y - 2)2 + (z + 1)2 9 và (x + 1)2 + (y - 2)2 + (z + 2)2 9 B. (x - 2)2 + (y - 2)2 + (z - 1)2 9 và x2 + y2 + (z + 3)2 9 C. (x + 2)2 + (y - 2)2 + (z + 1)2 9 và (x + 1)2 + (y - 2)2 + (z + 2)2 9 D. (x + 1)2 + (y - 2)2 + (z + 2)2 9 và (x - 2)...
Đọc tiếp
Trong không gian Oxyz, cho điểm A(1;0;-1), mặt phẳng (P): x + y - z - 3 = 0. Mặt cầu (S) có tâm I nằm trên mặt phẳng (P), đi qua điểm A và gốc tọa độ O sao cho chu vi tam giác OIA bằng 6 + √2. Phương trình mặt cầu (S) là:
A. (x + 2)2 + (y - 2)2 + (z + 1)2 = 9 và (x + 1)2 + (y - 2)2 + (z + 2)2 = 9
B. (x - 2)2 + (y - 2)2 + (z - 1)2 = 9 và x2 + y2 + (z + 3)2 = 9
C. (x + 2)2 + (y - 2)2 + (z + 1)2 = 9 và (x + 1)2 + (y - 2)2 + (z + 2)2 = 9
D. (x + 1)2 + (y - 2)2 + (z + 2)2 = 9 và (x - 2)2 + (y - 2)2 + (z - 1)2 = 9
Chọn D
Giả sử (S): x2 + y2 + z2 - 2ax - 2by - 2cz + d = 0 (a2 + b2 + c2 - d > 0)
và tâm I (a;b;c) ∈ (P) => a + b - c - 3 = 0 (1)
(S) qua A và O nên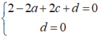 
Cộng vế theo vế (1) và (2) ta suy ra b = 2. Từ đó, suy ra I (a; 2; a-1)
Chu vi tam giác OAI bằng 6 + √2 nên OI + OA + AI = 6 + √2
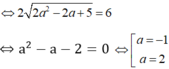
+ Với a = -1 => A (-1; 2; -2) => R = 3. Do đó:
+ Với a = 2 => I (2;2;1) => R = 3. Do đó:
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho điểm A(1;0;-1) và mặt phẳng (P): x+ y -z -3 0. Mặt cầu (S) có tâm I nằm trên mặt phẳng (P), đi qua điểm A và gốc tọa độ O sao cho chu vi tam giác OIA bằng 6 +
2
. Phương trình mặt cầu (S) là A.
x
+
2
2
+...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho điểm A(1;0;-1) và mặt phẳng (P): x+ y -z -3 =0. Mặt cầu (S) có tâm I nằm trên mặt phẳng (P), đi qua điểm A và gốc tọa độ O sao cho chu vi tam giác OIA bằng 6 + 2 . Phương trình mặt cầu (S) là
A. x + 2 2 + y - 2 2 + z + 1 2 = 9 và x + 1 2 + y - 2 2 + z + 2 2 = 9
B. x - 3 2 + y - 3 2 + z - 3 2 = 9 và x - 1 2 + y - 1 2 + z + 1 2 = 9
C. x + 2 2 + y - 2 2 + z - 1 2 = 9 và x 2 + y 2 + z + 3 2 = 9
D. x + 1 2 + y - 2 2 + z + 2 2 = 9 và x - 2 2 + y - 2 2 + z - 1 2 = 9
Đáp án D.
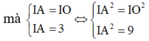
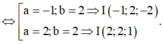
Vậy phương trình mặt cầu cần tìm là
Đúng 0
Bình luận (0)
Trong không gian với hệ trục tọa độ Oxyz, cho điểm A(1;0;-1) và mặt phẳng
P
:
x
+
y
-
z
-
3
0
. Gọi (S) là mặt cầu có tâm I nằm trên mặt phẳng (P), đi qua điểm A và gốc tọa độ O sao cho diện tích tam giác OIA bằng
17
2
. Tính bán kính R của mặt cầu (S) A. R 3 B. R 9 C. R 1 D. R 5
Đọc tiếp
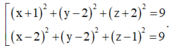
Trong không gian với hệ trục tọa độ Oxyz, cho điểm A(1;0;-1) và mặt phẳng P : x + y - z - 3 = 0 . Gọi (S) là mặt cầu có tâm I nằm trên mặt phẳng (P), đi qua điểm A và gốc tọa độ O sao cho diện tích tam giác OIA bằng 17 2 . Tính bán kính R của mặt cầu (S)
A. R = 3
B. R = 9
C. R = 1
D. R = 5
