Bài 3: Ôn tập chương Mặt nón, mặt trụ, mặt cầu

2:

\(\widehat{B'C;\left(A'B'C'\right)}=45^0\)

=>\(\widehat{\left(B'C;B'C'\right)}=45^0\)

=>\(\widehat{C'B'C}=45^0\)

Xét ΔCC'B' vuông tại C' có \(\widehat{C'B'C}=45^0\)

nên ΔCC'B' vuông cân tại C'

=>CC'=B'C'=a*căn 2

Thể tích khối lăng trụ là:

\(V=S_{BAC}\cdot CC'=a\sqrt{2}\cdot\dfrac{1}{2}a^2=\dfrac{\sqrt{2}}{2}\cdot a^3\)

\(\Delta ABC\) đều cạnh là mấy a ? 

Ta có: \(\left\{{}\begin{matrix}SH\perp AB\left(gt\right)\\CH\perp AB\left(\Delta ABC\text{ đều}\right)\end{matrix}\right.\) \(\Rightarrow AB\perp\left(SCH\right)\Rightarrow AB\perp SC\)

Từ A kẻ AD vuông góc SC (D thuộc SC)

\(\Rightarrow SC\perp\left(ADB\right)\Rightarrow\widehat{ADB}\) là góc giữa (SAC) và (SBC)

\(\Rightarrow\widehat{ADB}=90^0\)

\(\Rightarrow DH=\dfrac{1}{2}AB\) (trung tuyến ứng với cạnh huyền)

Lại có \(CH=\dfrac{AB\sqrt{3}}{2}\) (trung tuyến tam giác đều)

Áp dụng hệ thức lượng trong tam giác vuông SCH:

\(\dfrac{1}{DH^2}=\dfrac{1}{SH^2}+\dfrac{1}{CH^2}\Leftrightarrow\dfrac{4}{AB^2}=\dfrac{4}{3a^2}+\dfrac{4}{3AB^2}\)

\(\Rightarrow AB=a\sqrt{2}\)

\(\Rightarrow V=\dfrac{1}{3}SH.\dfrac{AB^2\sqrt{3}}{4}=\dfrac{a^3}{4}\)

Chọn B

Gọi chiều cao thùng là x (dm)

Thể tích nước trong thùng: \(V_1=3^2.8.\pi=72\pi\left(lít\right)\)

Thể tích quả cầu:  \(V_2=\dfrac{4}{3}\pi.3^3=36\pi\left(lít\right)\)

\(\Rightarrow\left(x-2\right).3^2.\pi=72\pi+36\pi\)

\(\Rightarrow x=14\left(dm\right)\)

\(\Rightarrow V=14.3^2.\pi=396\left(lít\right)\)

Thể tích nước trong thùng: V1=32.8.π=72π(lít)V1=32.8.π=72π(lít)

Thể tích quả cầu:  

?

Một cái thùng hình trụ có đường kính 60 cm. Người ta đổ vào thùng một lượng nước cao 80 cm. Sau đó thả vào thùng một quả cầu sắt có đường kính bằng đường kính của thùng, lúc này mực nước trong thùng dâng lên cách miệng thùng 20 cm. Tính dung tích của thùng.

Hình 1 không phải là hình đa diện.

Chọn D.

Bán kính đáy hình nón là a\(\sqrt{3}\)/3.

Diện tích xung quanh của hình nón cần tìm là \(\pi\).a\(\sqrt{3}\)/3.a = \(\pi\)a²\(\sqrt{3}\)/3.

Giả sử lượng bia ban đầu được chứa đầy trong lon.

Thể tích bia còn lại trong lon: V₁ = \(\pi\)3²h = 9\(\pi\)h.

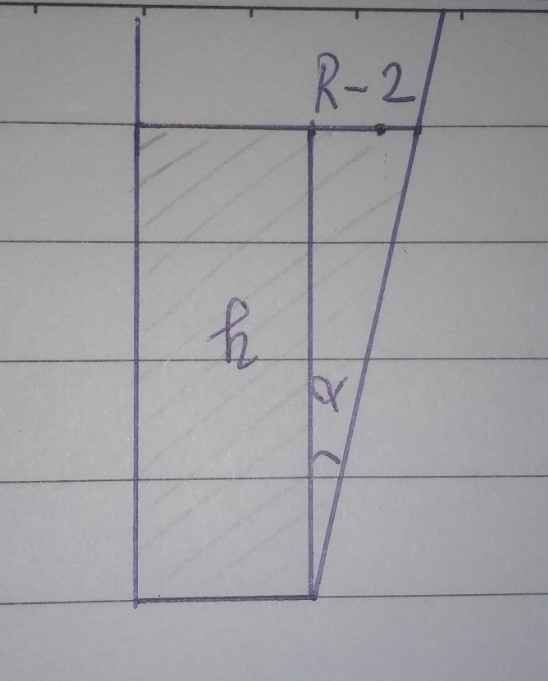
Thể tích bia trong ly sau khi đạt chiều cao h: V₂ = \(\pi\)h/3.(R²+2²+2R).

Ta có: tan\(\alpha\)=2/15=(R-2)/h, suy ra R=2/15.h+2.

Suy ra V₂ = 4\(\pi\)/3.(h³/225+h²/5+3h).

9\(\pi\)h + 4\(\pi\)/3.(h³/225+h²/5+3h) = \(\pi\)3².15 \(\Leftrightarrow\) 4h³+180h²+8775h-91125=0 \(\Rightarrow\) h gần bằng 8,58 (cm).

Chọn D.