Tìm tất cả các tiệm cận đứng của đồ thị hàm số y = 5 + x − 1 x 2 + 4 x
A. x = 0
B. Đồ thị hàm số không có tiệm cận đứng
C. x = -4
D. x = 0, x = -4
Cho hàm số
y
=
f
(
x
)
=
a
x
4
+
b
x
2
+
c
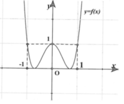
có đồ thị như hình bên dưới. Tìm tổng tất cả các đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
y
=
x
(
x
-
1
)
f
(
x
)
-
1
![]()
![]()
![]()
![]()
Cho hàm số y = f x = a x 4 + b x 2 + c có đồ thị như hình bên dưới. Tìm tổng tất cả các đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y = x x - 1 f x - 1
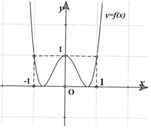
A. 4
B. 3
C. 2
D. 1
Tìm tất cả các tiệm cận đứng của đồ thị hàm số y = 2 x - 1 - x 2 + x + 3 x 2 - 5 x + 6
A. x= 3 và x= - 2.
B. x= -3
C. x= 3và x= 2.
D. x= 3
Tập xác định: D= R\ { 2; 3}
lim x → 2 + 2 x - 1 - x 2 + x + 3 x 2 - 5 x + 6 = lim x → 2 + ( 2 x - 1 ) 2 - ( x 2 + x + 3 ) ( x 2 - 5 x + 6 ) ( 2 x - 1 + x 2 + x + 3 ) = lim x → 2 + 3 x + 1 ( x - 3 ) ( 2 x - 1 + x 2 + x + 3 ) = - 7 6
Tương tự lim x → 2 - 2 x - 1 - x 2 + x + 3 x 2 - 5 x + 6 = - 7 6 .
Suy ra đường thẳng x= 2 không là tiệm cận đứng của đồ thị hàm số đã cho.
lim x → 3 + 2 x - 1 - x 2 + x + 3 x 2 - 5 x + 6 = + ∞ ; lim x → 3 - 2 x - 1 - x 2 + x + 3 x 2 - 5 x + 6 = - ∞
Suy ra đường thẳng x= 3 là tiệm cận đứng của đồ thị hàm số đã cho.
Chọn D.
Tìm tất cả các giá trị của tham số m để đồ thị hàm số y = x − 3 m x − 1 không có tiệm cận đứng
A. m = 0
B. m ≠ 0
C. m = 0 hoặc m = 1 3
D. m = 1 3
Đáp án D
Ta có: A ' C = A B 3 = a 3 ⇒ A B = a ⇐ V = a 3 .
Tìm tất cả các giá trị của tham số m để đồ thị hàm số y = x 2 − x − m x 2 − 4 có đúng một tiệm cận đứng và một tiệm cận ngang?
A. ∀ m ∈ ℝ \ 2 ; 6
B. ∀ m ∈ ℝ \ − 2 ; 2
C. m ∈ ℝ \ − 2 ; 2
D. m ∈ ℝ \ 2 ; 6
Đáp án D
Dễ thấy hàm số có 1 TCN y = 1.
Để hàm số có 1 TCĐ thì PT x 2 − x − m = 0 phải có 1 nghiệm x = 2 hoặc x= -2.
Vậy m ∈ 2 ; 6
Tìm tất cả các giá trị của tham số m để đồ thị hàm số y = x - 2 x 2 - m x + 1 có hai đường tiệm cận đứng
A. m ∈ ( - ∞ ; - 2 ) ∪ ( 2 ; + ∞ ) \ 5 2
B. m ∈ ( - ∞ ; - 2 ] ∪ [ 2 ; + ∞ )
C. m ∈ ( - ∞ ; - 2 ) ∪ ( 2 ; + ∞ )
D. m ≢ 5 2
tìm tất cả các giá trị thực của tham số m sao cho đồ thị của hàm số \(y=\dfrac{\sqrt{1-x}}{x-m}\) có tiệm cận đứng .
ĐKXĐ: \(x\le1\)
Hàm có tiệm cận đứng khi và chỉ khi phương trình:
\(x-m=0\) có nghiệm \(x< 1\)
\(\Leftrightarrow m< 1\)
Tìm tất cả các giá trị của tham số thực m để đồ thị hàm số y = x 2 x 2 − 2 x − m − x − 1 có hai tiệm cận đứng
A. m ≥ 4
B. − 5 < m ≤ 4
C. m > − 5
D. − 5 < m ≤ 4 m ≠ − 1
Tìm tất cả các giá trị của tham số thực m để đồ thị hàm số y = x 2 x 2 − 2 x − m − x − 1 có hai tiệm cận đứng
A. m ≥ 4
B. − 5 < m ≤ 4
C. m > − 5
D. − 5 < m ≤ 4 m ≠ − 1
Đáp án C
Ta có y = x 2 x 2 − 2 x − m + x + 1 x 2 − 4 x − m − 1
Điều kiện đặt ra là mẫu có 2 nghiệm => Δ ' = 5 + m > 0 < = > m > − 5