Trong không gian O x y z , cho hai vectơ a → 2 ; 1 ; − 3 , b → 2 ; 5 ; 1 . Mệnh đề nào dưới đây đúng ?
A. a → . b → = 4 .
B. a → . b → = 12 .
C. a → . b → = 6 .
D. a → . b → = 9 .
PB
Những câu hỏi liên quan
Trong không gian Oxyz, cho hai vectơ
u
→
(x; y; z),
v
→
(x; y; z). Khẳng định nào dưới đây sai? A.
u
→
x
2
+
y
2
+
z
2
B...
Đọc tiếp
Trong không gian Oxyz, cho hai vectơ u → = (x; y; z), v → = (x'; y'; z'). Khẳng định nào dưới đây sai?
A. u → = x 2 + y 2 + z 2
B. u → + v → = x + x ' ; y + y ' ; z + z '
C. u → . v → = x + y + z . x ' + y ' + z '
D. u → ⊥ v → ⇔ x . x ' + y . y ' + z . z ' = 0
Trong không gian Oxyz, cho hai vectơ
u
→
(x; y; z),
v
→
(x; y; z) khác
0
→
. Khẳng định nào dưới đây sai? A.
u
→
2
x
2
+
y
2
+
z
2...
Đọc tiếp
Trong không gian Oxyz, cho hai vectơ u → = (x; y; z), v → = (x'; y'; z') khác 0 → . Khẳng định nào dưới đây sai?
A. u → 2 = x 2 + y 2 + z 2 c
B. u → 2 = u → . v → ⇔ u → = v →
C. u → - v → = x - x ' ; y - y ' ; z - z '
D. cos u → ; v → = u → . v → u → . v →
Trong không gian Oxyz, cho hai vectơ
u
→
(
a
;
b
;
c
)
,
v
→
(
x
;
y
;
z
)
. Tích có hướng
[
u
→
,
v
→
]
có tọa độ là A. (bz-cy;cx-az;ay-bx). B. (bz+cy;cx+az;a...
Đọc tiếp
Trong không gian Oxyz, cho hai vectơ u → = ( a ; b ; c ) , v → = ( x ; y ; z ) . Tích có hướng [ u → , v → ] có tọa độ là
A. (bz-cy;cx-az;ay-bx).
B. (bz+cy;cx+az;ay+bx).
C. (by+cz;ax+cz;by+cz).
D. (bz-cy;az-cx;ay-bx)
Trong không gian Oxyz, cho vectơ
a
→
(-1; -2; 3). Tìm tọa độ của vectơ
b
→
(2; y; z) biết rằng vectơ
b
→
cùng phương với vectơ
a
→
A.
b
→
2
;
-...
Đọc tiếp
Trong không gian Oxyz, cho vectơ a → = (-1; -2; 3). Tìm tọa độ của vectơ b → = (2; y; z) biết rằng vectơ b → cùng phương với vectơ a →
A. b → = 2 ; - 2 ; 3
B. b → = 2 ; 4 ; 6
C. b → = 2 ; - 4 ; 6
D. b → = 2 ; 4 ; - 6
Đáp án D
Vectơ b → cùng phương với vectơ a → khi và chỉ khi tồn tại một số thực k thỏa mãn:
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz cho đường thẳng
d
:
x
-
1
2
y
-
2
1
z
+
1
2
nhận vectơ
u
→
a
;...
Đọc tiếp
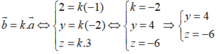
Trong không gian với hệ tọa độ Oxyz cho đường thẳng d : x - 1 2 = y - 2 1 = z + 1 2 nhận vectơ u → = a ; 2 ; b là vectơ chỉ phương. Tính a + b
A. - 8
B. 8
C. 4
D. - 4
Trong không gian với hệ tọa độ Oxyz, cho vectơ
a
→
(
-
1
;
-
2
;
3
)
. Tìm tọa độ của vectơ
b
→
(
2
;
y
;
z
)
, biết rằng vectơ
b
→
cùng phương với vectơ
a
→
.
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho vectơ a → = ( - 1 ; - 2 ; 3 ) . Tìm tọa độ của vectơ b → = ( 2 ; y ; z ) , biết rằng vectơ b → cùng phương với vectơ a → .
Trong không gian Oxyz, cho hai mặt phẳng (P):2x - y + z 0, (Q):x - z 0. Giao tuyến của hai mặt phẳng (P) và (Q) có một vectơ chỉ phương là: A.
a
⇀
(1; 0: -1) B.
a
⇀
(1; -3: 1) C.
a
⇀
(1; 3: 1) D.
a
⇀
(2; -1: 1)
Đọc tiếp
Trong không gian Oxyz, cho hai mặt phẳng (P):2x - y + z = 0, (Q):x - z = 0. Giao tuyến của hai mặt phẳng (P) và (Q) có một vectơ chỉ phương là:
A. a ⇀ = (1; 0: -1)
B. a ⇀ = (1; -3: 1)
C. a ⇀ = (1; 3: 1)
D. a ⇀ = (2; -1: 1)
Trong không gian Oxyz cho hai vectơ
x
→
2
;
1
;
-
3
,
y
→
1
;
0
;
-
1
. Tìm tọa độ của vectơ
a
→
x...
Đọc tiếp
Trong không gian Oxyz cho hai vectơ x → 2 ; 1 ; - 3 , y → 1 ; 0 ; - 1 . Tìm tọa độ của vectơ a → = x → + 2 y →
Trong không gian với hệ tọa độ Oxyz cho các vectơ
a
→
(1;2;1),
b
→
(-2;3;4),
c
→
(0;1;2),
d
→
(4;2;0). Biết
d
→
x.
a
→
+y.
b
→
+z.
c
→
. Tổng x+y+z là A. 2 B. 3 C. 5 D. 4
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz cho các vectơ a → =(1;2;1), b → =(-2;3;4), c → =(0;1;2), d → =(4;2;0). Biết d → =x. a → +y. b → +z. c → . Tổng x+y+z là
A. 2
B. 3
C. 5
D. 4
Trong không gian với hệ trục tọa độ Oxyz, cho hai đường thẳng
d
1
:
x
-
4
3
y
-
1
-
1
z
+
5
-
2
và...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho hai đường thẳng d 1 : x - 4 3 = y - 1 - 1 = z + 5 - 2 và d 2 : x - 2 1 = y + 3 3 = z 1 . Giả sử A ∈ d 1 , B ∈ d 2 sao cho AB là đoạn vuông góc chung của d1 và d2. Vectơ A B ⇀ là:
A. A B ⇀ = ( 5 ; - 5 ; 10 )
B. A B ⇀ = ( 2 ; - 2 ; 4 )
C. A B ⇀ = ( 3 ; - 3 ; 6 )
D. A B ⇀ = ( 1 ; - 1 ; 2 )
