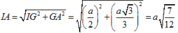Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a , A B C ⏞ = 60 0 , cạnh bên SA vuông góc với đáy SA= a 3 Tính thể tích của khối chóp S.ABCD
A. a 3 4 .
B. a 3 3 6
C. a 3 2
D. a 3 3 3
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, ABC = 60 ° cạnh bên SA = a 2 và SA vuông góc với ABCD. Tính góc giữa SB và (SAC).
A. 90 °
B. 30 °
C. 45 °
D. 60 °
Chọn B.
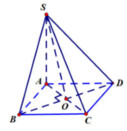
Gọi O = AC ∩ BD. Vì ABCD là hình thoi nên BO ⊥ AC(1). Lại do:
![]()
Từ (1) và (2) ta có:BO ⊥ (SAC)
![]()
Ta có: ![]()
Vì ABCD là hình thoi có ABC = 60 ° nên tam giác ABC đều cạnh a
![]()
Trong tam giác vuông SBO ta có:
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, góc ABC=60°. Cạnh bên SA vuông góc với mặt đáy và cạnh bên SC tạo với mặt đáy một góc 60°. Gọi I là trung điểm BC, H là hình chiếu vuông góc của A lên SI. Tính thể tích khối chóp S.ABCD và khoảng cách từ điểm H đến (SCD) theo a.
a) Dễ dàng chứng minh tam giác ABC và ACD đều
Suy ra AC=a, SA= AC.tan(gócSCA)=a.tan(600)
\(V_{S.ABCD}=\frac{1}{3}.SA.S_{ABCD}=\frac{1}{3}.a\sqrt{3}.a^2.\frac{\sqrt{3}}{2}=\frac{a^3}{2}\)
b) Có 2 cách làm để tìm khoảng cách từ H đến mp(SCD), nhưng bạn nên chọn phương pháp tọa độ hóa cho dễ
Chọn A làm gốc tọa độ , các tia AD, AI, AS lần lượt trùng tia Ax, Ay, Az
Có ngay tọa độ các điểm \(S\left(0;0;a\sqrt{3}\right)\) , \(D\left(a;0;0\right)\) , \(I\left(0;\frac{a\sqrt{3}}{2};0\right)\)
\(\Rightarrow C\left(\frac{a}{2};\frac{a\sqrt{3}}{2};0\right)\)
theo số liệu đã cho, dễ xác định được điểm H chia đoạn SI với tỷ lệ 2:1
\(\Rightarrow H\left(0;\frac{a}{\sqrt{3}};\frac{a}{\sqrt{3}}\right)\)
Bây giờ chỉ cần viết pt (SCD) là tính được ngay khoảng cách từ H đến SCD
\(\left(SCD\right):\sqrt{3}x+y+z-\sqrt{3}=0\)
\(d\left(H\text{/}\left(SCD\right)\right)=\frac{a\sqrt{3}}{\sqrt{5}}\)
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, A B C ^ = 120 0 .Cạnh bên S A = 3 a và SA vuông góc với (ABCD) .Tính a theo Vcủa khối chóp S.ABCD?
A. V = a 3 2
B. V = a 3 4
C. V = 3 a 3 4
D. V = 3 a 3 2
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, A B C ^ = 60 ° . Mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính diện tích của mặt cầu ngoại tiếp hình chóp S.ABCD.
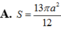
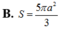
![]()
![]()
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a. Cạnh bên SA vuông góc với đáy (ABCD) và SA=3a. Tính bán kính R của mặt cầu ngoại tiếp khối chóp S.ABCD
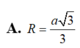
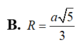
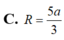
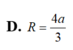
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và SA = SB = SC = a.
Góc giữa mặt bên hình chóp S.ABCD và mặt phẳng đáy có tang bằng:
A. 1
B. 3
C. 3 2
D. Đáp án khác
Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông cạnh AB = a (a>0) Góc giữa mặt bên và mặt đáy bằng 60 ° Tính thể tích khối chóp S.ABCD:
A. a 3 3 2
B. a 3 6
C. a 3 3 3
D. a 3 3 6
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và góc ∠ A B C = 60 ° , cạnh bên SA=a và vuông góc với mặt đáy. Tính bán kính R của mặt cầu ngoại tiếp tứ diện S.ACD.
A. R = a 5 2
B. R = a
C. R = a 7 12
D. R = a 2
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và góc A B C ^ = 60 ° , cạnh bên SA=a và vuông góc với mặt đáy. Tính bán kính R của mặt cầu ngoại tiếp tứ diện S.ACD
A. R = a 5 2
B. R = a
C. R = a 7 12
D. R = a 2
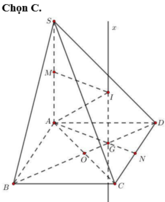
Ta có A D C ^ = A B C ^ = 60 ° , suy ra tam giác ADC là tam giác đều cạnh a. Gọi N là trung điểm cạnh DC, G là trọng tâm của tam giác ABC. Ta có A N = a 3 2 ; A G = a 3 3
Trong mặt phẳng (SAN), kẻ đường thẳng Gx//SA, suy ra Gx là trục của tam giác ADC.
Gọi M là trung điểm cạnh SA. Trong mặt phẳng (SAN) kẻ trung trực của SA cắt Gx tại I thì IS=IA=ID=IC nên I chính là tâm mặt cầu ngoại tiếp tứ diện S.ACD. Bán kính R của mặt cầu bằng độ dài đoạn IA.
Trong tam giác AIG vuông tại G, ta có: