Biết tổng các hệ số trong khai triển nhị thức Newton của 5 x − 1 n bằng 2 100 . Tìm hệ số của x 3
A. − 161700
B. -19600
C. -2450000
D. -20212500
PB
Những câu hỏi liên quan
Biết tổng các hệ số trong khai triển nhị thức Newton của
(
5
x
-
1
)
n
bằng
2
100
. Tìm hệ số của
x
3
. A. -161700 B. -19600 C. -20212500 D. -2450000
Đọc tiếp
Biết tổng các hệ số trong khai triển nhị thức Newton của ( 5 x - 1 ) n bằng 2 100 . Tìm hệ số của x 3 .
A. -161700
B. -19600
C. -20212500
D. -2450000
Chọn D
Ta có,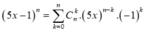 
.
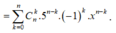Tổng các hệ số trong khai triển ( 5 x - 1 ) n bằng 2 100 nên ta có phương trình:
.
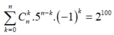
Vậy
(
5
x
-
1
)
n
.
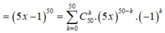
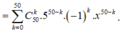Xét số hạng chứa x 3 thì 50 - k = 3 => k = 47.
=> Hệ số của số hạng chứa
x
3
là: 
.
Đúng 0
Bình luận (0)
Tìm hệ số của
x
5
trong khai triển nhị thức Newton
x
x
+
1
x
3
n
,
biết tổng các hệ số của khai triển bằng 128 A. 37. B. 36. C. 35. D. 38.
Đọc tiếp
Tìm hệ số của x 5 trong khai triển nhị thức Newton x x + 1 x 3 n , biết tổng các hệ số của khai triển bằng 128
A. 37.
B. 36.
C. 35.
D. 38.
Tìm hệ số của
x
5
trong khai triển nhị thức Newton
x
x
+
1
x
3
n
, biết tổng các hệ số của khai triển bằng 128 A. 37 B. 36 C. 35 D. 38
Đọc tiếp
Tìm hệ số của x 5 trong khai triển nhị thức Newton x x + 1 x 3 n , biết tổng các hệ số của khai triển bằng 128
A. 37
B. 36
C. 35
D. 38
Tìm hệ số của số hạng chứa x trong khai triển (2+3x) mũ 5 ( sử dụng công thức tổng quát Nhị Thức Newton)
SHTQ của \(\left(3x+2\right)^5\) là \(C^k_5\cdot\left(3x\right)^{5-k}\cdot2^k=C^k_5\cdot3^{5-k}\cdot2^k\cdot x^{5-k}\)
Hệ số của số hạng chứa x tương ứng với 5-k=1
=>k=4
=>Hệ số là \(C^4_5\cdot3^{5-4}\cdot2^4=240\)
Đúng 1
Bình luận (0)
Biết rằng trong khai triển nhị thức Newton của
x
+
1
x
n
tổng các hệ số của hai số hạng đầu bằng 24. Gọi S là tổng các hệ số của số hạng chứa
x
k
k
0
. Hỏi S có tính chất gì trong các tính chất sau? A. S là một số nguyên tố. B. S...
Đọc tiếp
Biết rằng trong khai triển nhị thức Newton của x + 1 x n tổng các hệ số của hai số hạng đầu bằng 24. Gọi S là tổng các hệ số của số hạng chứa x k k > 0 . Hỏi S có tính chất gì trong các tính chất sau?
A. S là một số nguyên tố.
B. S là một lũy thừa của 24
C. S là một số chính phương
D. S là một số lập phương đúng.
Ta có x + 1 x n = ∑ k = 0 n C n k x n - 2 k
Theo đề ta có C n 0 + C n 1 = 24 ⇔ 1 + n = 24 ⇔ n = 23
Số hạng chứa x mũ nguyên dương thỏa n - 2 k > 0 ⇔ k < n 2 = 23 2
Do k ∈ Z nên k ∈ 1 ; 2 ; 3 ; . . 11 .
Suy ra có 12 số hạng chứa x mũ nguyên dương
Đáp án C
Đúng 0
Bình luận (0)
Biết rằng trong khai triển nhị thức Newton của
x
+
1
x
n
tổng các hệ số của hai số hạng đầu bằng 24. Gọi S là tổng các hệ số của số hạng chứa
x
k
k
0
. Hỏi S có tính chất gì trong các tính chất sau? A. S là một số nguyên...
Đọc tiếp
Biết rằng trong khai triển nhị thức Newton của x + 1 x n tổng các hệ số của hai số hạng đầu bằng 24. Gọi S là tổng các hệ số của số hạng chứa x k k > 0 . Hỏi S có tính chất gì trong các tính chất sau?
A. S là một số nguyên tố
B. S là một lũy thừa của 24
C. S là một số chính phương
D. S là một số lập phương đúng
Biết rằng hệ số của
x
3
trong khai triển nhị thức Newton
2
x
2
+
1
x
n
(với
x
≠
0
) bằng
2
6
C
n
9
. Tìm n. A....
Đọc tiếp
Biết rằng hệ số của x 3 trong khai triển nhị thức Newton 2 x 2 + 1 x n (với x ≠ 0 ) bằng 2 6 C n 9 . Tìm n.
A. n =12
B. n =13
C. n =14
D. n =15
Trong khai triển nhị thức Newton của\({(2x + 3)^5}\) , hệ số của \({x^4}\) hay hệ số của \({x^3}\) lớn hơn?
Ta có:
\({(2x + 3)^5} = 32{x^5} + 240{x^4} + 720{x^3} + 1080{x^2} + 810x + 243\)
Hệ số của \({x^3}\) là 720
Hệ số của \({x^4}\) là 240.
Vậy hệ số của \({x^3}\) lớn hơn hệ số của \({x^4}\).
Đúng 0
Bình luận (0)
Biết rằng hệ số của
x
4
trong khai triển nhị thức Newton
2
-
x
n
,
n
∈
ℕ
*
bằng 280. Tìm n. A.
n
8
B.
n...
Đọc tiếp
Biết rằng hệ số của x 4 trong khai triển nhị thức Newton 2 - x n , n ∈ ℕ * bằng 280. Tìm n.
A. n = 8
B. n = 6
C. n = 7
D. n = 5
