Cho hình chóp tứ giác đều S.ABCD có cạnh đáy 3 2 a , bằng cạnh bên bằng 5a. Tính bán kính R của mặt cầu ngoại tiếp hình chóp S.ABCD.
A. R = 3 a .
B. R = 2 a .
C. R = 25 8 a .
D. R = 2 a .
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, góc giữa cạnh bên và mặt phẳng đáy bằng 600. Tính thể tích khối chóp S.ABCD.
A. a 3 6
B. a 3 6 3
C. a 3 6 6
D. a 3 6 2
Đáp án C
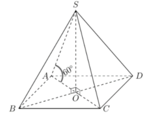
Gọi O là tâm đáy ABCD. Khi đó S O ⊥ A B C D
suy ra AO là hình chiếu vuông góc của SA lên mặt phẳng đáy. Khi đó góc giữa cạnh bên SA và đáy là S A O ^
Suy ra S A O ^ = 60 °
Vậy thể tích khối chóp là:
V = 1 3 . S O . S A B C D = a 3 6 6
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, cạnh bên hợp với đáy một góc 30 ° .Thể tích V của khối chóp S.ABCD bằng
A. V = a 3 6 9 .
B. V = a 3 6 18 .
C. V = a 3 3 9 .
D. V = a 3 3 6 .
Đáp án B.
Chiều cao khối chóp:
h = a 2 2 . tan 30 ° = a 6 6 .
Do đó
V = 1 3 a 2 . h = 1 3 a 2 . a 6 6 = 6 a 3 18 .
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, góc giữa cạnh bên và mặt phẳng đáy bằng 60 0 . Tính thể tích khối chóp S.ABCD.
A. a 3 6 2
B. a 3 6 6
C. a 3 6
D. a 3 6 3
Đáp án B
Ta có: 2 B I 2 = a 2 ⇒ B I = a 2 ; S I = B I tan 60 0 = a 3 2
Thể tích khối chóp S.ABCD là
V = 1 3 S I . S A B C D = 1 3 a 3 2 . a 2 = a 3 6 6
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, góc giữa cạnh bên và mặt phẳng đáy bằng 60 0 . Tính thể tích khối chóp S.ABCD
A. a 3 6 2
B. a 3 6 6
C. a 3 6
D. a 3 6 3
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a cạnh bên hợp với mặt đáy một góc 600. Tính theo a thể tích khối chóp S.ABCD.
A. V = 6 a 3 6
B. V = 6 a 3 2
C. V = 6 a 3 3
D. V = a 3 3
Chọn A.
Gọi H là tâm của hình vuông ABCD thì SH ⊥ (ABCD)
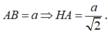
Do đó
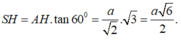
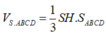
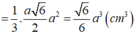
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, cạnh bên hợp với mặt đáy một góc 60 ° . Tính theo a thể tích khối chóp S.ABCD
A. V = a 3 6 6
B. V = a 3 6 2
C. V = a 3 6 3
D. V = a 3 3
Cho hình chóp tứ giác đều S.ABCD cạnh đáy bằng cạnh bên bằng a.
A. 54 o 73 '
B. 35 o 15 '
C. 54 o 44 '
D. không phải các kết quả A, B, C
Từ O dựng , suy ra N là trung điểm của BC.
Hai mặt phẳng (SBC) và (ABCD) cắt nhau theo giao tuyến BC
Và O N ⊥ B C ; S N ⊥ B C
Suy ra: ( S B C ) ; ( A B C D ) ^ = S N O ^
Ta có: O N = 1 2 A B = a 2 ;
Tam giác SBC có SB = SC = BC =a nên là tam giác đều ; đường cao S N = a 3 2
cos S N O ^ = O N S N = a 2 a 3 2 = 1 3 ⇒ S N O ^ ≈ 54 0 44 '
Đáp án C
Cho hình chóp tứ giác đều S.ABCD cạnh đáy bằng cạnh bên bằng a. Góc giữa cạnh bên và mặt phẳng đáy bằng:
A. 60 o
B. 30 o
C. 45 o
D. không phải các kết quả A, B, C
Gọi O là giao điểm của AC và BD.
Vì S, ABCD là hình chóp tứ giác đều nên
Hình chiếu vuông góc của điểm S lên mp(ABCD) là điểm O nên góc giữa cạnh bên và mặt phẳng đáy là góc SBO.
Ta có: B D = a 2 ; B O = 1 2 B D = a 2
Lại có: S B 2 + S D 2 = B D 2 = 2 a 2 nên tam giác SBD vuông cân tại S. ⇒ S B O ^ = 45 0
Đáp án C
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, góc ABC bằng , cạnh bên SA vuông góc với đáy, SC tạo với đáy góc 60 o . Tính thể tích khối chóp S.ABCD.
A. a 3 2
B. a 3 3
C. a 3 5
D. a 3 2 2
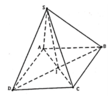
Ta có:
A C = a ⇒ S A = A C tan 60 o = a 3 B D = 2 B I = 2 . B C . sin 60 o = a 3 V = 1 3 S A . S A B C D = 1 3 . S A . 1 2 . A C . B D
Đáp án A