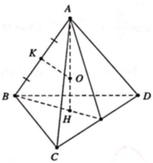
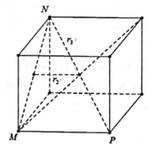
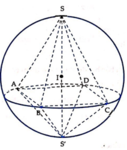
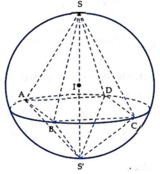
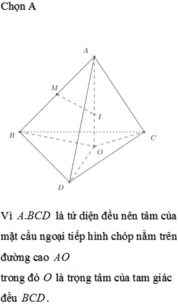
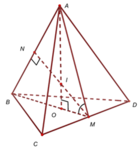
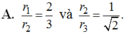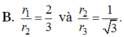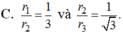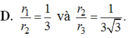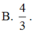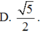Cho tứ diện đều ABCD có mặt cầu nội tiếp là S 1 và mặt cầu ngoại tiếp là S 2 . Một hình lập phương ngoại tiếp S 2 và nội tiếp trong mặt cầu S 2 . Gọi r 1 , r 2 , r 3 lần lượt là bán kính các mặt cầu ( S 1 ) , ( S 2 ) , ( S 3 ) . Khẳng định nào sau đây đúng?
A. r 1 r 2 = 2 3 và r 2 r 3 = 1 2 .
B. r 1 r 2 = 2 3 và r 2 r 3 = 1 3 .
C. r 1 r 2 = 1 3 và r 2 r 3 = 1 3 .
D. r 1 r 2 = 1 3 và r 2 r 3 = 1 3 3 .