Các câu hỏi tương tự
Một mặt cầu có tâm nằm trong tứ diện đều cạnh a và mặt cầu đó tiếp xúc với 6 cạnh của tứ diện đó. Tính diện tích S của mặt cầu.
Đọc tiếp
Một mặt cầu có tâm nằm trong tứ diện đều cạnh a và mặt cầu đó tiếp xúc với 6 cạnh của tứ diện đó. Tính diện tích S của mặt cầu.
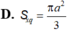
Một hình chóp tứ giác đều có cạnh đáy bằng cạnh bên và bằng a. Tính diện tích S của mặt cầu ngoại tiếp hình chóp
Đọc tiếp
Một hình chóp tứ giác đều có cạnh đáy bằng cạnh bên và bằng a. Tính diện tích S của mặt cầu ngoại tiếp hình chóp
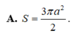
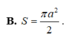
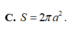
![]()
Một hình chóp tứ giác đều có cạnh đáy bằng cạnh bên và bằng a. Tính diện tích S của mặt cầu ngoại tiếp hình chóp.
Đọc tiếp
Một hình chóp tứ giác đều có cạnh đáy bằng cạnh bên và bằng a. Tính diện tích S của mặt cầu ngoại tiếp hình chóp.
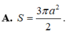
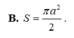
![]()
![]()
Tính diện tích S của mặt cầu ngoại tiếp tứ diện AB’C’D’ biết ABCDA’B’C’D’ là hình lập phương cạnh a
Đọc tiếp
Tính diện tích S của mặt cầu ngoại tiếp tứ diện AB’C’D’ biết ABCDA’B’C’D’ là hình lập phương cạnh a
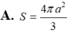
![]()
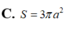
![]()
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu
S
:
x
−
1
2
+
y
2
+
z
−
2
2
9
ngoại tiếp khối bát diện (H) được ghép từ hai khối chóp tứ giác đều S.ABCD và S’.ABCD (đều có đáy là tứ giác...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu S : x − 1 2 + y 2 + z − 2 2 = 9 ngoại tiếp khối bát diện (H) được ghép từ hai khối chóp tứ giác đều S.ABCD và S’.ABCD (đều có đáy là tứ giác ABCD). Biết rằng đường tròn ngoại tiếp của tứ giác ABCD là giao tuyến của mặt cầu (S) và mặt phẳng P : 2 x + 2 y − z − 8 = 0 . Tính thể tích khối bát diện (H)
A. V H = 34 9 .
B. V H = 665 81 .
C. V H = 68 9 .
D. V H = 1330 81 .
Mặt cầu ngoại tiếp hình chóp tứ giác đều có tất cả các cạnh bằng a có diện tích là: A. S
4
πa
2
B. S
2
2
πa
2
C. S
2
πa
2
D. S
3
πa
2
2
Đọc tiếp
Mặt cầu ngoại tiếp hình chóp tứ giác đều có tất cả các cạnh bằng a có diện tích là:
A. S = 4 πa 2
B. S = 2 2 πa 2
C. S = 2 πa 2
D. S = 3 πa 2 2
Diện tích mặt cầu ngoại tiếp hình chóp tứ giác đều có tất cả các cạnh bằng
a
A.
2
πa
2
3
B.
2
πa
2
C.
4
πa
2
3
D.
4
π...
Đọc tiếp
Diện tích mặt cầu ngoại tiếp hình chóp tứ giác đều có tất cả các cạnh bằng a
A. 2 πa 2 3
B. 2 πa 2
C. 4 πa 2 3
D. 4 πa 2
Cho tứ diện ABCD có CDa
2
,
∆
ABC là tam giác đều cạnh a,
∆
ACD vuông tại A. Mặt phẳng (BCD) vuông góc với mặt phẳng (ABD). Thể tích khối cầu ngoại tiếp tứ diện ABCD bằng
Đọc tiếp
Cho tứ diện ABCD có CD=a 2 , ∆ ABC là tam giác đều cạnh a, ∆ ACD vuông tại A. Mặt phẳng (BCD) vuông góc với mặt phẳng (ABD). Thể tích khối cầu ngoại tiếp tứ diện ABCD bằng
![]()
![]()
![]()
![]()
Cho tứ diện ABCD có
C
D
a
2
,
∆
A
B
C
là tam giác đều cạnh a,
∆
A
C
D
vuông tại A. Mặt phẳng (BCD) vuông góc với mặt phẳng (ABD). Thể tích của khối cầu ngoại tiếp tứ diện ABCD bằng A.
4
πa
3
3
B. ...
Đọc tiếp
Cho tứ diện ABCD có C D = a 2 , ∆ A B C là tam giác đều cạnh a, ∆ A C D vuông tại A. Mặt phẳng (BCD) vuông góc với mặt phẳng (ABD). Thể tích của khối cầu ngoại tiếp tứ diện ABCD bằng
A. 4 πa 3 3
B. πa 3 6
C. 4 πa 3
D. πa 3 3 2