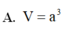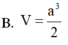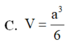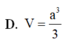Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác cân tại C, AA'=a, B A C ^ = 30 0 , A B = a 3 . Gọi M là trung điểm của BB'. Tính theo a thể tích V của khối tứ diện MACC'
A. V = a 3 3 12
B. V = a 3 3 4
C. V = a 3 3 3
D. V = a 3 3 18
PB
Những câu hỏi liên quan
Cho hình lăng trụ đứng ABC.ABC có đáy ABC là tam giác cân tại A,
B
A
C
^
120
0
,
B
C
A
A
3
a
. Tính thể tích V của khối lăng trụ ABC.ABC. A.
V
9
a
3...
Đọc tiếp
Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác cân tại A, B A C ^ = 120 0 , B C = A A ' = 3 a . Tính thể tích V của khối lăng trụ ABC.A'B'C'.
A. V = 9 a 3 4
B. V = 3 3 a 3 2
C. V = 3 3 a 3 6
D. V = 3 a 3 4
Đáp án D
Ta có: B C 2 = A B 2 + A C 2 − 2 A B . A C cos A = 2 A B 2 − 2 A B 2 cos 120 0 = 3 A B 2 ⇒ A B = A C = a
S A B C = 1 2 . a 2 sin 120 0 = 3 a 2 4
. Thể tích lăng trụ là: V = A A ' . S A B C = 3 a . 3 a 2 4 = 3 a 3 4
Đúng 0
Bình luận (0)
Cho hình lăng trụ đứng ABC.ABC có đáy ABC là tam giác cân tại A,
B
A
C
⏜
120
0
, BCAA
3
a
. Tính thể tích V của khối lăng trụ ABC.ABC
Đọc tiếp
Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác cân tại A, B A C ⏜ = 120 0 , BC=AA'= 3 a . Tính thể tích V của khối lăng trụ ABC.A'B'C'
Cho hình lăng trụ đứng
A
B
C
.
A
B
C
có đáy ABC là tam giác cân tại A,
B
A
C
^
120
°
,
B
C
A
A
3
a
. Tính theo a thể tích V của khối lăng trụ
A
B
C
.
A
B
C
A. ...
Đọc tiếp
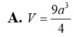
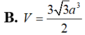
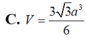
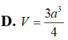
Cho hình lăng trụ đứng A B C . A ' B ' C ' có đáy ABC là tam giác cân tại A, B A C ^ = 120 ° , B C = A A ' = 3 a . Tính theo a thể tích V của khối lăng trụ A B C . A ' B ' C '
A. V = 9 a 3 4
B. V = 3 3 a 3 2
C. V = 3 6 a 3 6
D. V = 3 a 3 4
Đáp án D
Phương pháp:
Thể tích khối lăng trụ: V = Sh, trong đó: S là diện tích đáy, h là chiều cao.
Cách giải:
Đúng 0
Bình luận (0)
Cho hình lăng trụ đứng ABC.ABC có đáy ABC là tam giác cân tại A, và
BAC
^
120
°
,
BC
AA
3
a
. Tính theo a thể tích V của khối lăng trụ ABC.ABC A.
V
9
a
3
4...
Đọc tiếp
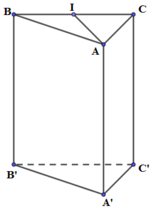
Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác cân tại A, và BAC ^ = 120 ° , BC = AA ' = 3 a . Tính theo a thể tích V của khối lăng trụ ABC.A'B'C'
A. V = 9 a 3 4
B. V = 3 3 a 3 6
C. V = 3 3 a 3 2
D. V = 3 a 3 4
a) Cho hình lăng trụ đứng ABC.ABC có đáy ABC là tam giác vuông cân tại A, ABa. Biết diện tích tứ giác ABBA bằng 2a^2, thể tích khối lăng trụ ABC.ABC bằng? b) Cho hình lăng trụ đúng ABC.ABC có đáy ABC là tam giác vuông cân tại A, ABa. Biết góc giữa (ABC) và (ABC) bằng 60°, thể tích khối lăng trụ ABC.ABC bằng?
Đọc tiếp
a) Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông cân tại A, AB=a. Biết diện tích tứ giác ABB'A' bằng \(2a^2\), thể tích khối lăng trụ ABC.A'B'C' bằng?
b) Cho hình lăng trụ đúng ABC.A'B'C' có đáy ABC là tam giác vuông cân tại A, AB=a. Biết góc giữa (AB'C') và (A'B'C') bằng 60°, thể tích khối lăng trụ ABC.A'B'C' bằng?
a: BB'=2a^2:a=2a
V=BB'*S ABC
=2a*1/2a^2
=a^3
Đúng 0
Bình luận (0)
Cho hình lăng trụ đứng ABC.ABC có đáy ABC là tam giác cân tại A,
B
A
C
^
120
o
và BC AA a
3
. Tính theo a thể tích V của khối lăng trụ ABC.ABC. A.
V
9
a
3
4...
Đọc tiếp
Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác cân tại A, B A C ^ = 120 o và BC =AA' = a 3 . Tính theo a thể tích V của khối lăng trụ ABC.A'B'C'.
A. V = 9 a 3 4
B. V = 3 3 a 3 6
C. V = 3 3 a 3 2
D. V = 3 a 3 4
Cho hình lăng trụ đứng ABC.ABC có đáy ABC là tam giác cân tại C, BAC 30
°
, AB a
3
, AA a. Gọi M là trung điểm của BB. Tính theo a thể tích V của khối tứ diện MACC. A. V
a
3
3
12
B. V
a
3
3
4
C....
Đọc tiếp
Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác cân tại C, BAC = 30 ° , AB = a 3 , AA' = a. Gọi M là trung điểm của BB'. Tính theo a thể tích V của khối tứ diện MACC'.
A. V = a 3 3 12
B. V = a 3 3 4
C. V = a 3 3 3
D. V = a 3 3 18
Cho lăng trụ đứng ABC.ABC có AAa đáy ABC là tam giác vuông cân tại A và ABa. Tính thể tích V của khối lăng trụ đã cho.
Đọc tiếp
Cho lăng trụ đứng ABC.A'B'C' có AA'=a đáy ABC là tam giác vuông cân tại A và AB=a. Tính thể tích V của khối lăng trụ đã cho.
Cho lăng trụ đứng
A
B
C
.
A
B
C
có đáy là tam giác ABC vuông cân tại A,
A
B
a
,
A
A
a
3
. Tính bán kính R của mặt cầu đi qua tất cả các đỉnh của hình lăng trụ theo a. A.
R
a
2...
Đọc tiếp
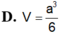
Cho lăng trụ đứng A B C . A ' B ' C ' có đáy là tam giác ABC vuông cân tại A, A B = a , A A ' = a 3 . Tính bán kính R của mặt cầu đi qua tất cả các đỉnh của hình lăng trụ theo a.
A. R = a 2 2
B. R = a 2
C. R = a 5 2
D. R = 2a
Phương pháp:
Xác định tâm đường tròn ngoại tiếp O, O ' của hai tam giác đáy. Khi đó, tâm mặt cầu ngoại tiếp hình lăng trụ là trung điểm của OO’.
Cách giải:
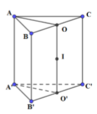
Do tam giác ABC vuông cân tại A nên trung điểm O của BC là tâm đường tròn ngoại tiếp tam giác ABC.
Tương tự, trung điểm O’ của B’C’ là tâm đường tròn ngoại tiếp tam giác A’B’C’.
Khi đó, tâm mặt cầu I ngoại tiếp hình lăng trụ là trung điểm của OO’.
Đúng 0
Bình luận (0)
Cho khối lăng trụ đứng ABC.ABC có AAa, đáy ABC là tam giác vuông cân tại A và BC
a
2
. Tính thể tích V của khối lăng trụ đã cho
Đọc tiếp
Cho khối lăng trụ đứng ABC.A'B'C' có AA'=a, đáy ABC là tam giác vuông cân tại A và BC= a 2 . Tính thể tích V của khối lăng trụ đã cho
