Cho cấp số nhân u n c ó u 1 = 2 và biểu thức 20 u 1 − 10 u 2 + u 3 đạt giá trị nhỏ nhất. Số hạng thứ bảy của cấp số nhân u n có giá trị bằng
A. 6250
B. 31250
C. 136250
D. 39062
Cho các số hạng dương a, b, c là số hạng thứ m, n, p của một cấp số cộng và một cấp số nhân. Tính giá trị của biểu thức log 2 a b - c b c - a c a - b
A. 0
B. 2
C. 1
D. 4
Cho cấp số nhân u n có u 1 = 2 và biểu thức 20 u 1 - 10 u 2 + u 3 đạt giá trị nhỏ nhất. Số hạng thứ bảy của cấp số nhân u n có giá trị bằng
A. 31250
B. 6250
C. 136250
D. 39062
Phát biểu định nghĩa cấp số nhân và công thức tổng n số hạng đầu tiên của một cập số nhân.
+ Định nghĩa: Cấp số nhân là một dãy số (hữu hạn hoặc vô hạn), trong đó từ số hạng thứ hai; mỗi số hạng đều là tích các số hạng đứng ngay trước nó với một số không đổi q.
Số q được gọi là công bội của cấp số nhân.
(un) : un + 1 = un.q.
+ Tổng n số hạng đầu tiên của CSN.
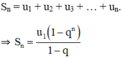
Bài 1: Cho cấp số nhân có: u3 = 18 và u6 = -486.
Tìm số hạng đầu tiên và công bội q của cấp số nhân đó
Bài 2: Tìm u và q của cấp số nhân (un) biết:
Bài 3: Tìm cấp số nhân (un) biết cấp số đó có 4 số hạng có tổng bằng 360 và số hạng cuối gấp 9 lần số hạng thứ hai.
có những các hình thức đấu tranh của giai cấp tư sản(giai cấp công nhân) nào? hình thức nào tiêu biểu nhất vì sao?
- Những hình thức đấu tranh của giai cấp tư sản:
+ Đập phá máy móc
+ Lập công đoàn
+ Đấu tranh chống áp bức bóc lột
- Hình thức tiêu biểu: Đứng lên đấu tranh, nổi dậy chống áp bức
Giai cấp vô sản kh phải giai cấp tư sản mình ghi nhầm
Ai đó làm ơn giúp mình với ạ, mình cảm ơn rất nhiều 1.Cho cấp số nhân(Un). Tìm U1 và q. Biết rằng a. U1 + u6= 165; u3 + u4=60 2. Tìm số hạng đầu và công bội của cấp số nhân, biết a. U4- u2= 72; U5- u3=144 b. u1- u3+u5=65;u1+u7=325 c. u3+u5=90; u2-u6=240 d. u1+u2+u3=14; u1.u2.u3=64
Để tìm U1 và q, ta sử dụng hệ phương trình sau:
U1 + U6 = 165U3 + U4 = 60Đầu tiên, ta sử dụng phương trình thứ hai để tìm U3: U3 = 60 - U4
Sau đó, thay giá trị của U3 vào phương trình thứ nhất: U1 + U6 = 165 U1 + (U3 + 3q) = 165 U1 + (60 - U4 + 3q) = 165 U1 - U4 + 3q = 105 (1)
Tiếp theo, ta sử dụng phương trình thứ nhất để tìm U6: U6 = 165 - U1
Thay giá trị của U6 vào phương trình thứ hai: U3 + U4 = 60 (60 - U4) + U4 = 60 60 = 60 (2)
Từ phương trình (2), ta thấy rằng phương trình không chứa U4, do đó không thể giải ra giá trị của U4. Vì vậy, không thể tìm được giá trị cụ thể của U1 và q chỉ từ hai phương trình đã cho.
Để tìm số hạng đầu và công bội của cấp số nhân, ta sử dụng các phương trình đã cho:
a. U4 - U2 = 72 U5 - U3 = 144
Đầu tiên, ta sử dụng phương trình thứ nhất để tìm U4: U4 = U2 + 72
Sau đó, thay giá trị của U4 vào phương trình thứ hai: U5 - U3 = 144 (U2 + 2q) - U3 = 144 U2 - U3 + 2q = 144 (3)
Từ phương trình (3), ta thấy rằng phương trình không chứa U2, do đó không thể giải ra giá trị của U2 và q chỉ từ hai phương trình đã cho.
b. U1 - U3 + U5 = 65 U1 + U7 = 325
Đầu tiên, ta sử dụng phương trình thứ hai để tìm U7: U7 = 325 - U1
Sau đó, thay giá trị của U7 vào phương trình thứ nhất: U1 - U3 + U5 = 65 U1 - U3 + (U1 + 6q) = 65 2U1 - U3 + 6q = 65 (4)
Từ phương trình (4), ta thấy rằng phương trình không chứa U3, do đó không thể giải ra giá trị của U1 và q chỉ từ hai phương trình đã cho.
c. U3 + U5 = 90 U2 - U6 = 240
Đầu tiên, ta sử dụng phương trình thứ hai để tìm U6: U6 = U2 - 240
Sau đó, thay giá trị của U6 vào phương trình thứ nhất: U3 + U5 = 90 U3 + (U2 - 240 + 4q) = 90 U3 + U2 - 240 + 4q = 90 U3 + U2 + 4q = 330 (5)
Từ phương trình (5), ta thấy rằng phương trình không chứa U2, do đó không thể giải ra giá trị của U2 và q chỉ từ hai phương trình đã cho.
d. U1 + U2 + U3 = 14 U1 * U2 * U3 = 64
Đầu tiên, ta sử dụng phương trình thứ nhất để tìm U3: U3 = 14 - U1 - U2
Sau đó, thay giá trị của U3 vào phương trình thứ hai: U1 * U2 * (14 - U1 - U2) = 64
Phương trình này có dạng bậc ba và không thể giải ra giá trị cụ thể của U1 và U2 chỉ từ hai phương trình đã cho.
Tóm lại, không thể tìm được giá trị cụ thể của số hạng đầu và công bội của cấp số nhân chỉ từ các phương trình đã cho.
Câu 1 : Cho biểu thức A= \(\dfrac{a^3+2a^2-1}{a^3+2a^2+2a+1}\)
a, Rút gọn biểu thức
b, Chứng minh rằng nếu a là số nguyên thì giá trị của biểu thức tìm được của câu a, là một phân số tối giản.
Câu 2:Tìm tất cả các số tự nhiên có 3 chữ số \(\overline{abc}\) sao cho \(\overline{abc}\) = \(n^2-1\) và \(\overline{cba}=\left(n-2\right)^2\)
Trả lời nhanh giùm mk câu hỏi này nhá!
Mai Ngọc Trâm
Câu 1 : Câu hỏi của Hoàng Nguyễn Xuân Dương - Toán lớp 6 - Học toán với OnlineMath
Câu 2 :
Ta có : abc = 100 x a + 10 x b + c = n2 ‐ 1 ﴾1﴿
cba = 100 x c + 10 x b + a = n2 ‐ 4n + 4 ﴾2﴿
Lấy ﴾1﴿ trừ ﴾2﴿ ta được :
99 x ﴾a – c﴿ = 4n – 5
Suy ra 4n ‐ 5 chia hết 99
Vì 100 \(\le\) abc \(\le\) 999 nên :
100 ≤ n2 ‐1 ≤ 999 => 101 ≤ n2 ≤ 1000 => 11 ≤ 31 => 39 ≤ 4n ‐ 5 ≤ 119
Vì 4n ‐ 5 chia hết 99 nên 4n ‐ 5 = 99 => n = 26 => abc = 675
Câu 1: Ta có: A= \(\dfrac{a^3+2a^2-1}{a^3+2a^2+2a+1}\) =\(\dfrac{\left(a+1\right)\left(a^2+a-1\right)}{\left(a+1\right)\left(a^2+a+1\right)}=\dfrac{a^2+a-1}{a^2+a+1}\)
a. Điều kiện đúng \(a\ne-1\)
Rút gọn biểu thức \(\dfrac{a^2+a-1}{a^2+a+1}\)
b. Gọi d là ƯCLN của a2 + a - 1 và a2 + a - 1 và a2 + a + 1
Vì a2 + a - 1 = a ( a + 1 ) - 1 là số lẻ nên d là số lẻ
Mặt khác 2 =[ a2+a +1 – (a2 + a – 1) ] chia hết d
Nên d = 1 tức là a2 + a + 1 và a2 + a - 1 nguyên tố cùng nhau
Câu 2: \(\overline{\text{abc}}\) = 100a + 10 b + c = n2 - 1 (1)
\(\overline{\text{cba}}\) = 100c + 10 b + c = n2 – 4n + 4 (2)
Từ (1) và (2) \(\Rightarrow\) 99(a-c) = 4 n – 5 \(\Rightarrow\) 4n – 5 chia hết 99 (3)
Mặt khác: 100[ n2-1[999\(\Leftrightarrow\)101 [n2 [1000\(\Leftrightarrow\)11 [n[31\(\Leftrightarrow\)39[4n-5
[119] (3)
Từ (3) và (4) \(\Rightarrow\) 4n – 5 = 99 \(\Rightarrow\) n = 26
Vậy: \(\overline{\text{abc}}\) = 675
Câu 1 : Cho biểu thức \(A=\dfrac{a^3+2a^2-1}{a^3+2a^2+2a+1}\)
a) Rút gọn biểu thức
b) Chứng minh rằng nếu a là số nguyên thì giá trị của biểu thức tìm được của câu a, là một phân số tối giản
Câu 2 :
a) Tìm n để \(n^2+2006\) là 1 số chính phương
b) Cho n là số nguyên tố lớn hơn 3. Hỏi \(n^2+2006\) là số nguyên tố hay hợp số
Câu 1 mình làm rồi, bạn tìm trong câu hỏi tương tự ấy.
Câu 2:
a) Đặt \(n^2+2006=a^2\left(a\in Z\right)\)
\(\Rightarrow2006=a^2-n^2=\left(a-n\right)\left(a+n\right)\)
Mà \(\left(a+n\right)-\left(a-n\right)=2n⋮2\)
\(\Rightarrow a+n\) và \(a-n\) có cùng tính chẵn, lẻ
Nếu \(a+n\) và \(a-n\) cùng lẻ \(\Rightarrow\left(a-n\right)\left(a+n\right)\) lẻ (loại)
Nếu \(a+n\) và \(a-n\) cùng chẵn \(\Rightarrow\left(a-n\right)\left(a+n\right)⋮4\) (loại)
Vậy không có số nguyên \(n\) nào thỏa mãn \(n^2+2006\) là số chính phương
b) Vì \(n\) là số nguyên tố lớn hơn \(3\Rightarrow n\) \(⋮̸\) \(3\)
\(\Rightarrow\left[\begin{matrix}n=3k+1\\n=3k+2\end{matrix}\right.\)\(\left(k\ne0\right)\)
Nếu \(n=3k+1\Rightarrow n^2+2006=\left(3k+1\right)^2+2006\)
\(=9k^2+6k+2007⋮3;>3\Rightarrow n\) là hợp số
Nếu \(n=3k+2\Rightarrow n^2+2006=\left(3k+2\right)^2+2006\)
\(=9k^2+12k+2010⋮3;>3\Rightarrow n\) là hợp số
Vậy \(n^2+2006\) là hợp số
Câu 1: Cho biểu thức:
A=\(\dfrac{ }{A=\dfrac{a^{3^{ }}+2a^2-1}{a^3+2a^2+2a+1}}\)
a, Rút gọn biểu thức
b, Chứng minh rằng nếu a là số nguyên thì giá trị của biểu thức tìm được của câu a, là một phân số tối giản.