Cho số thực a > 4. Gọi P là tích tất cả các nghiệm của phương trình a lnx 2 - a ln ( ex ) + a = 0 . Khi đó
A. P = ae
B. P = e
C. P = a
D . P = a e
Cho số thực a > 4 . Gọi P là tích tất cả các nghiệm của phương trình a ln x 2 - a ln 6 x + a = 0 . Khi đó
![]()
![]()
![]()
![]()
Cho phương trình sin x + m 2 3 + sin 2 x - m 2 3 = 2 sin x - m 2 3 . Gọi S = [a;b] là tập hợp tất cả các giá trị thực của tham số m để phương trình trên có nghiệm thực. Tìm giá trị của P = a 2 + b 2
A. P = 162 49
B. P = 49 162
C. P = 4
D. P = 2
Cho phương trình e m . cos x - sin x - e 2 1 - sin x = 2 - sin x - m . cos x với m là tham số thực. Gọi S là tập hợp tất cả các giá trị của m để phương trình có nghiệm. Khi đó S=( - ∞ ; a ] ∪ [ b ; + ∞ ). Tính T=10a+20b
A. 10 3
B . 0
C. 19
D. -1
Gọi A là tập tất cả các giá trị thực của tham số m sao cho tập nghiệm của phương trình x . 2 x = x x - m + 1 + m 2 x - 1 có hai phần tử.Tìm số phần tử của A.
A. 1
B. Vô số
C. 3
D. 2
Đáp án D
Ta có x . 2 x = x x - m + 1 + m 2 x - 1 ⇔ x . 2 x = x 2 - m x + x + m . 2 x - m
⇔ 2 x x - m = x + 1 x - m ⇔ 2 x - x - 1 x - m = 0 ⇔ [ 2 x - x - 1 = 0 ( 1 ) x - m = 0 ( 2 )
Giải (1) , đặt f x = 2 x - x - 1 . Xét hàm số f x = 2 x - x - 1 trên ℝ , có f ' x = 2 x . ln 2 - 1
Phương trình f ' x = 0 ⇔ 2 x = 1 ln 2 ⇔ x = log 2 1 ln 2 = - log 2 ln 2
⇒ f x = 0 có nhiều nhất 2 nghiệm mà f 0 = f 1 ⇒ f x = 0 ⇔ [ x = 0 x = 1
Để phương trình đã cho có hai nghiệm phân biệt ⇔ 2 có 1 nghiệm hoặc 0
Vậy m = {0;1} là hai giá trị cần tìm.
Gọi A là tập tất cả các giá trị thực của tham số m sao cho tập nghiệm của phương trình x .2 x = x x − m + 1 + m 2 x − 1 có hai phần tử. Tìm số phần tử của A.
A. 1
B. Vô số
C. 3
D. 2
Gọi A là tập tất cả các giá trị thực của tham số m sao cho tập nghiệm của phương trình x .2 x = x x − m + 1 + m 2 x − 1 có hai phần tử. Tìm số phần tử của A.
A. 1
B. 2
C. 3
D. Vô số
Gọi A là tập tất cả các giá trị thực của tham số m sao cho tập nghiệm của phương trình x . 2 x = x x - m + 1 + m 2 x - 1 có hai phần tử. Tìm số phần tử của A.
A. 1
B. 2
C. 3
D. Vô số
Đáp án B.
Ta có x . 2 x = x x - m + 1 + m 2 x - 1 ⇔ x - m 2 x = x 2 - ( m - 1 ) x - m
⇔ x - m 2 x = ( x - m ) ( x + 1 ) ⇔ x - m 2 x - x - 1 = 0 ⇔ x = m 2 x = x + 1
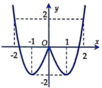
Giải phương trình 2 x = x + 1 .
![]()
Nhìn vào màn hình ta thấy phương trình 2 x = x + 1 có hai nghiệm phân biệt là x = 0 ; x = 1 . Do vậy để tập nghiệm của phương trình đã cho có đúng hai phần tử thì m ∈ 0 ; 1 . Vậy có 2 giá trị của m thỏa mãn, ta chọn B.
Gọi A là tập tất cả các giá trị thực của tham số m sao cho tập nghiệm của phương trình x.2x = x(x - m +1) + m(2x - 1) có hai phần tử.Tìm số phần tử của A.
A. 1
B. Vô số
C. 3
D. 2
Đáp án D
Ta có

Giải (1) , đặt f(x) = 2x - x - 1. Xét hàm số f(x) = 2x - x - 1trên R, có f’(x) = 2x.ln2 - 1
Phương trình
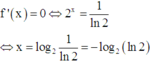
=> f(x) = 0 có nhiều nhất 2 nghiệm mà f(0) = f(1) => f(x) = 0 <=> x = 0 hoặc x = 1
Để phương trình đã cho có hai nghiệm phân biệt <=> (2) có 1 nghiệm hoặc 0
Vậy m = {0 ;1} là hai giá trị cần tìm.
Cho phương trình m . l n 2 ( x + 1 ) - ( x + 2 - m ) l n ( x + 1 ) - x - 2 = 0 (1). Tập hợp tất cả các giá trị của tham số m để phương trình (1) có hai nghiệm phân biệt thoả mãn 0 < x 1 < 2 < 4 < x 2 là khoảng . Khi đó a thuộc khoảng
![]()
![]()
![]()
![]()