Cho hàm số y = f ( x ) = ax 4 + bx 3 + cx 2 + dx + e . Biết rằng hàm số y = f’(x) liên tục trên R và có đồ thị như hình bên. Hỏi hàm số y = f ( 2 x - x 2 ) có bao nhiêu điểm cực đại
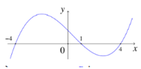
A. 5
B. 3
C. 1
D. 2
Cho hàm số y=f(x)=x^3+ax^2+bx+4 có đồ thị (C) như hình vẽ. Hỏi (C) là đồ thị của hàm số y=f(x) nào?
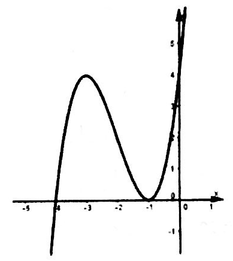
A. y = f ( x ) = x 3 - 3 x 2 + 4
B. y = f ( x ) = x 3 + 6 x 2 + 9 x + 4
C. y = f ( x ) = x 3 + 3 x 2 + 4
D. y = f ( x ) = x 3 - 6 x 2 + 9 x + 4
a) Cho hàm số y=f(x)=ax5+bx3+cx-5 (a,b,c thuộc R)
Cho f(-3)=208. Tính f(3)=?
b) Cho hàm số y=g(x)=ax4-bx2+x+3 (a,b thuộc R)
Cho g(2)=17. Tính g(-2)=?
Cho hàm số y= f(x)= ax^2+bx+c
Tìm a,b,c nếu biết f(0)=2; f(2)=3; f(3)=4.
cho hàm số y=f(x) =ax^3+bx+7 . Biết f(6)=1. Tính f(-6)
cho hàm số y=f(x)=\(ax^2+bx+C\)
Tìm a,b,c nếu biết f(0)=2;f(2)=3;f(3)=4
Cho hàm số y=ax^5+bx^3+cx-5. Biết f(-3)=208. Tính f(x)
cho hàm số y=f(x)=ax^2+bx+c. tìm a,b,c biết : f(0)=3; f(1)=0; f(3)=0
LÀM XONG NHỚ T.I.C.K Á
F(0)=3 =>C=3
F(1)=0=>A+B+C=0=>A+B= -3 (1)
F(-1)=1=>A+B+C=1=>A-B= -2 (2)
KẾT HỢP 1 VÀ 2 =>A=5/2;B=1/2
Cho hàm số \(y=f\left(x\right)=ax^2+bx+c\)
Xác định các hệ số \(a,b,c\) biết \(f\left(0\right)=1\),\(f\left(1\right)=2\),\(f\left(2\right)=4\)
Giúp mình với :3?
f(0) = 1
\(\Rightarrow\) a.02 + b.0 + c = 1
\(\Rightarrow\) c = 1
Vậy hệ số a = 0; b = 0; c = 1
f(1) = 2
\(\Rightarrow\) a.12 + b.1 + c = 2
\(\Rightarrow\) a + b + c = 2
Vậy hệ số a = 1; b = 1; c = 1
f(2) = 4
\(\Rightarrow\) a.22 + b.2 + c = 4
\(\Rightarrow\) 4a + 2b + c = 4
Vậy hệ số a = 4; b = 2; c = 1
Chúc bn học tốt! (chắc vậy :D)
Cho hàm số y=f(x)=ax^2+bx+c
Biết f(0)=3 , f(1)=0, f(-1)=1.Tìm a,b.c?
f(0)=3 =>c=3
f(1)=0 => a+b+c=0 =>a+b=-3 (1)
f(-1)=1 => a-b+c=1 =>a-b=-2 (2)
Kết hợp (1) và (2) => a=-5/2 ; b=-1/2
cho hàm số y=f(x)=ax^2+bx+c.Tim a,b,c biết f(-2)=0;f(2)=0 và a-c=3
Ta có: \(y=f\left(x\right)=ax^{2\:}+bx+c\)
\(\Rightarrow f\left(-2\right)=4a-2b+c=2a-2b+2a+c=2a-2b+3c+6=0\)
\(\Rightarrow2a-2b+3c=-6\left(1\right)\)
\(f\left(2\right)=4a+2b+c=2a+2b+2a+c=2a+2b+3c+6=0\)
\(\Rightarrow2a+2b+3c=-6\left(2\right)\)
Từ (1)(2) \(\Rightarrow2a-2b+3c=2a+2b+3c\)
\(\Rightarrow2a-2b+3c-\left(2a+2b+3c\right)=0\)
\(\Rightarrow2a-2b+3c-2a-2b-3c=0\)
\(\Rightarrow\left(2a-2a\right)-\left(2b+2b\right)+\left(3c-3c\right)=0\)
\(\Rightarrow-4b=0\)
\(\Rightarrow b=0\)
\(\Rightarrow2a+3c=-6\)
\(\Rightarrow5c+6=-6\)
\(\Rightarrow5c=-12\)
\(\Rightarrow c=\frac{-12}{5}\)
\(\Rightarrow a=\frac{-12}{5}+3=\frac{3}{5}\)
Vậy \(a=\frac{3}{5};c=\frac{-12}{5};b=0\)