Vẽ (d) : y= x+3
(d') : y = -2x-3
Tìm tọa độ giao điểm bằng ptoán
NN
Những câu hỏi liên quan
(d):y=(m+1)x+3, (d'):y=2x+3
tìm tọa độ giao điểm của (d) và (d')
Tọa độ giao điểm của `(d)` và `(d')` là:
`(m+1)x+3=2x+3`
`<=>mx+x+3-2x-3=0`
`<=>mx-x=0`
`<=>x(m-1)=0`
`<=>[(x=0),(m=1 (loại)):}`
`=>y=2.0+3=0+3=3`
`=>` Tọa độ giao điểm của `(d)` và `(d')` là `(0;3)`.
Đúng 3
Bình luận (0)
Vẽ (d1) : y = 2x+2
(d2) : y = x-1
Tìm tọa độ gđ bằng ptoán
PT hoành độ giao điểm: \(2x+2=x-1\Leftrightarrow x=-3\Leftrightarrow y=-4\Leftrightarrow A\left(-3;-4\right)\)
Vậy \(A\left(-3;-4\right)\) là giao điểm 2 đths
Đúng 0
Bình luận (0)
1/ Vẽ (D) và (P) trên cùng một hệ trục tọa độ a) (D) : y= -2x + 3 b) (P) : y = x² c) Tìm tọa độ giao điểm của hai đồ thị 2/ Vẽ (D) và (P) trên cùng một hệ trục tọa độ a) (D) : y= -x + 3 b) (P) : y = 2x² c) Tìm tọa độ giao điểm của hai đồ thị 3/ Vẽ (D) và (P) trên cùng một hệ trục tọa độ a) (D) : y= x - 3 b) (P) : y = -3x² c) Tìm tọa độ giao điểm của hai đồ thị
1:
a: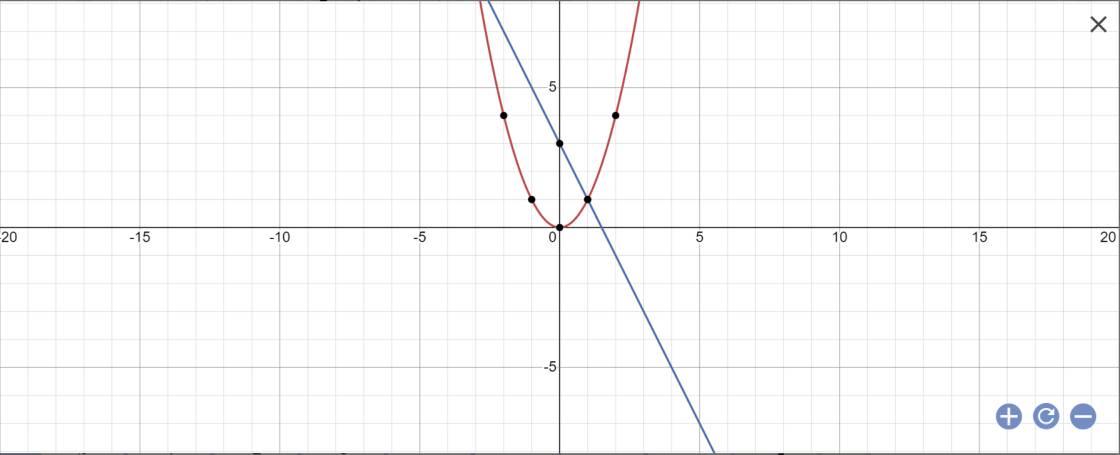 
b: PTHĐGĐ là:
x^2+2x-3=0
=>(x+3)(x-1)=0
=>x=-3 hoặc x=1
=>y=9 hoặc y=1
Đúng 0
Bình luận (0)
Cho hàm số y=x+3 (d); y=2x+1 (d')
a)Vẽ đồ thị của 2 hàm số trên cùng 1 hệ trục tọa độ
b)Tìm tọa độ giao điểm của d và d' bằng phép tính
b: Phương trình hoành độ giao điểm là:
2x+1=x+3
=>2x-x=3-1
=>x=2
Thay x=2 vào y=x+3, ta được:
y=2+3=5
a: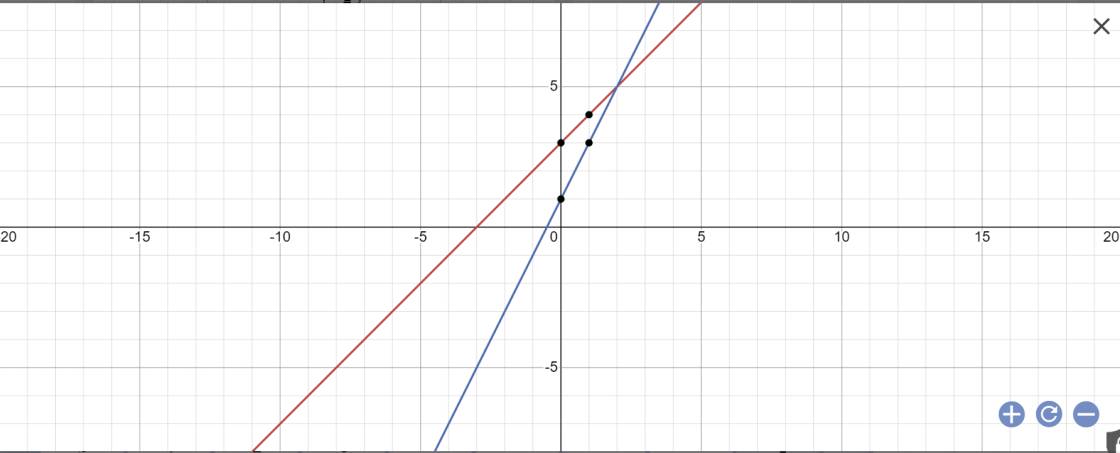 
Đúng 2
Bình luận (0)
Cho (D) : y = 2x – 5 và (D’) : y = – 1 2 x. a/ Vẽ (D) và (D’) trên cùng 1 mặt phẳng tọa độ. b/ Tìm tọa độ giao điểm M của (D) và (D’) bằng phép tính.
\(b,\text{PT hoành độ giao điểm: }2x-5=-\dfrac{1}{2}x\Leftrightarrow\dfrac{5}{2}x=5\Leftrightarrow x=2\Leftrightarrow y=-1\Leftrightarrow M\left(2;-1\right)\)
Đúng 0
Bình luận (0)
Vẽ (P): y=\(\dfrac{x^2}{3}\) và (D): y=2x-3; tìm tọa độ giao điểm của (P) và (D)
Xét ptr hoành độ của `(P)` và `(D)` có:
`x^2/3=2x-3`
`<=>x^2=6x-9`
`<=>x^2-6x+9=0`
`<=>(x-3)^2=0`
`<=>x-3=0<=>x=3`
`=>y=2.3-3=3`
Vậy tọa độ giao điểm của `(P)` và `(D)` là: `(3;3)`
Đúng 1
Bình luận (0)
a) Vẽ (P): \(y=-2x^2\);(D):\(y=x-3\)
b) Tìm tọa độ giao điểm
b) PTHĐGĐ của (P) và (d)
\(-2x^2=x-3\\ \Leftrightarrow2x^2+x-3=0\\ \Leftrightarrow\left(x-1\right)\left(2x+3\right)=0\\ \left[{}\begin{matrix}x=1\\x=\dfrac{-3}{2}\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}y=-2\\y=-\dfrac{9}{2}\end{matrix}\right.\)
Vậy (d) cắt (P) tại 2 điểm A(1,-2) ,B(\(-\dfrac{3}{2},-\dfrac{9}{2}\))
Đúng 0
Bình luận (4)
Cho 2 hàm số y=x² ; y= -2x+3 có đồ thị lần lượt là Parabol (P) và đường thẳng (D) a) Vẽ (P) và (D) trên cùng mặt phẳng tọa độ b) Tìm tọa độ giao điểm của (P) và (D) bằng phép toán
a)
\(\left(P\right):y=x^2\)
Ta có bảng
| x | -2 | -1 | 0 | 1 | 2 |
| y | 4 | 1 | 0 | 1 | 4 |
Vậy đồ thị hàm số \(y=x^2\) là một parabol lần lượt đi qua các điểm
\(\left(-2;4\right),\left(-1;1\right),\left(0;0\right),\left(1;1\right),\left(2;4\right)\)
Bạn tự vẽ nhé
\(\left(d\right):y=-2x+3\)
Cho \(y=0\Rightarrow x=\dfrac{3}{2}\Rightarrow A\left(\dfrac{3}{2};0\right)\in Ox\)
Cho \(x=0\Rightarrow y=3\Rightarrow B\left(0;3\right)\in Oy\)
Vẽ đường thẳng AB ta được đths \(y=-2x+3\)
Bạn tự bổ sung vào hình vẽ nhé
b) Xét PTHĐGĐ của \(\left(P\right),\left(d\right)\) là nghiệm của phương trình
\(x^2=-2x+3\\ \Leftrightarrow x^2+2x-3=0\)
Xét \(a+b+c=1+2-3=0\\ \Rightarrow\left[{}\begin{matrix}x=1\\x=-3\end{matrix}\right.\)
Với `x=1 => y=x^2 = 1`
Với `x=2 => y=x^2 = 4`
Vậy tọa độ giao điểm của \(\left(P\right),\left(d\right)\) là 2 điểm \(\left(1;1\right)\) và \(\left(2;4\right)\)
Đúng 2
Bình luận (0)
Cho parabol (P):y=x2 và đường thẳng (d):y=2x+m
a) Vẽ (P) và (d) trên cùng mặt phẳng tọa độ với m=3. Tìm tọa độ giao điểm của (d) và (P) (bằng lập luận và bằng đồ thị)
b) Tìm m để (d) tiếp xúc với (P). Xác định tọa độ tiếp điểm
giúp mình đi vẽ hộ cái hình
cho đường tròn tâm O bán kính r,điểm A cố định nằm ngoài đường tròn.kẻ 2 tiếp tuyến AM,AN.Đường thẳng D đi qua A cắt đường tròn O tại B,C với AB<AC.Chứng minh 5 điểm A,M,N,O,I thuộc đường tròn