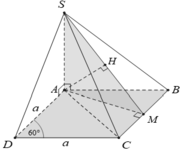
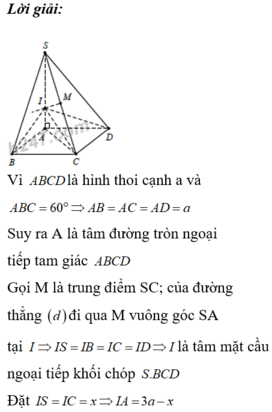
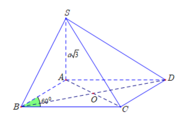
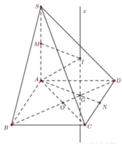
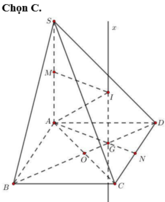
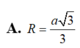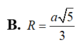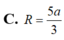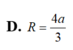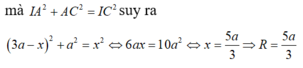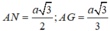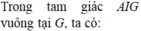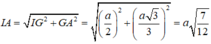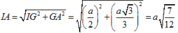Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, B A D ^ = 60 ° và SA vuông góc với mặt phẳng (ABCD). Góc giữa 2 mặt phẳng (SBD) và (ABCD) bằng 450. Gọi M là điểm đối xứng của C qua B và N là trung điểm của SC. Mặt phẳng (MND) chia khối chóp S.ABCD thành hai khối đa diện, trong đó khối đa diện chứa đỉnh S có thể tích V1, khối đa diện còn lại có thể tích V2 (tham khảo hình vẽ bên). Tính tỉ số V 1 V 2

A. V 1 V 2 = 12 7
B. V 1 V 2 = 5 3
C. V 1 V 2 = 1 5
D. V 1 V 2 = 7 5