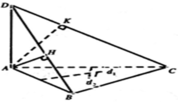
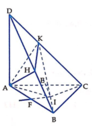
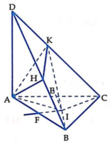
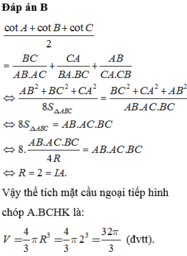
Cho tứ diện ABCD có A D ⊥ ( A B C ) , đáy ABC thỏa mãn điều kiện c o t A + c o t B + c o t C 2 = B C A B . A C + C A B C . B A + A B C A . C B . Gọi H, K lần lượt là hình chiếu vuông góc của A lên DB và DC. Tính thể tích V của khối cầu ngoại tiếp khối chóp A.BCHK
A. V = 32 π 3
B. V = 8 π 3
C. V = 4 π 3 3
D. V = 4 π 3