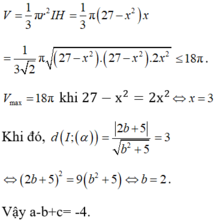Trong không gian Oxyz gọi ∆ là giao tuyến của hai mặt phẳng α : x - 3 y + z = 0 ; β : x + y - z + 4 = 0 . Véctơ nào dưới đây là một véctơ chỉ phương của ∆ ?
A. u 1 ⇀ 4 ; 2 ; 2
B. u 2 ⇀ 2 ; 2 ; 4
C. u 3 ⇀ 2 ; 4 ; 2
D. u 4 ⇀ 2 ; 2 ; 2
PB
Những câu hỏi liên quan
Trong không gian với hệ trục tọa độ Oxyz, gọi (α) là mặt phẳng chứa đường thẳng
∆
:
x
-
2
1
y
-
1
1
z
-
2
và vuông góc với mặt phẳng (β):x+y+2z+10. Khi đó giao tuyến của hai mặt phẳng (α), (β) có phương trình A. ...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, gọi (α) là mặt phẳng chứa đường thẳng ∆ : x - 2 1 = y - 1 1 = z - 2 và vuông góc với mặt phẳng (β):x+y+2z+1=0. Khi đó giao tuyến của hai mặt phẳng (α), (β) có phương trình
A. x - 1 = y + 1 1 = z - 1
B. x 1 = y + 1 1 = z - 1 1
C. x - 2 1 = y + 1 - 5 = z 2
D. x + 2 1 = y - 1 - 5 = z 2
Trong không gian với hệ tọa độ Oxyz viết phương trình đường thẳng giao tuyến của hai mặt phẳng
α
:
x
+
3
y
-
z
+
1
0
;
β
:
2
x
-
y
+
z
-
7
0
. A.
x
+
2
2...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz viết phương trình đường thẳng giao tuyến của hai mặt phẳng α : x + 3 y - z + 1 = 0 ; β : 2 x - y + z - 7 = 0 .
A. x + 2 2 = y - 3 = z + 3 - 7
B. x - 2 2 = y 3 = z - 3 - 7
C. x - 2 = y - 3 - 3 = z - 10 7
D. x - 2 - 2 = y 3 = z - 3 7
Ta có:
+) Tìm tọa độ điểm A x 0 ; y 0 ; z 0 thuộc hai mặt phẳng α ; β :
Chọn y 0 = 0 ⇒ x 0 ; z 0 là nghiệm của hệ phương trình:
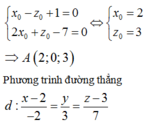
Chọn D.
Đúng 0
Bình luận (0)
Trong không gian Oxyz, có đường thẳng d là giao tuyến của hai mặt phẳng
P
:
x
+
y
+
z
3
và
Q
:
x
-
y
+
z
5
. Mặt phẳng (α) chứa đường thẳng d và đi qua gốc tọa độ có phương trình là A.
x
+
4
y
+
z
0
B....
Đọc tiếp
Trong không gian Oxyz, có đường thẳng d là giao tuyến của hai mặt phẳng P : x + y + z = 3 và Q : x - y + z = 5 . Mặt phẳng (α) chứa đường thẳng d và đi qua gốc tọa độ có phương trình là
A. x + 4 y + z = 0
B. 5 x + 4 y + z = 0
C. x - 4 y + z = 0
D. 5 x - 4 y + z = 0
Trong không gian Oxyz, coh đường thẳng d là giao tuyến của hai mặt phẳng
P
:
x
+
y
+
z
3
và
P
:
x
-
y
+
z
5
. Mặt phẳng
α
chứa đường thẳng d và đi qua gốc tọa độ có phương trình là A.
x
+
4
y
+
z
0
B....
Đọc tiếp
Trong không gian Oxyz, coh đường thẳng d là giao tuyến của hai mặt phẳng P : x + y + z = 3 và P : x - y + z = 5 . Mặt phẳng α chứa đường thẳng d và đi qua gốc tọa độ có phương trình là
A. x + 4 y + z = 0
B. 5 x + 4 y + z = 0
C. x - 4 y + z = 0
D. 5 x - 4 y + z = 0
Chọn đáp án A.
Cách 1: Đường thẳng d có một vectơ chỉ phương là
Cách 2: Vì mặt phẳng α chứa đường thẳng d nên α có phương trình
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho điểm A(0;1;2), mặt phẳng (α): x-y+z-40 và mặt cầu (S): (x-3)²+ (y-1)²+ (z-2)²16. Gọi (P) là mặt phẳng đi qua A, vuông góc với (α) và đồng thời (P) cắt mặt cầu (S) theo giao tuyến là một đường tròn có bán kính nhỏ nhất. Tọa độ giao điểm M của (P) và trục xOx là:
A
.
M
-
1
2
;
0
;...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho điểm A(0;1;2), mặt phẳng (α): x-y+z-4=0 và mặt cầu (S): (x-3)²+ (y-1)²+ (z-2)²=16. Gọi (P) là mặt phẳng đi qua A, vuông góc với (α) và đồng thời (P) cắt mặt cầu (S) theo giao tuyến là một đường tròn có bán kính nhỏ nhất. Tọa độ giao điểm M của (P) và trục x'Ox là:
A . M - 1 2 ; 0 ; 0
B . M - 1 3 ; 0 ; 0
C . M 1 ; 0 ; 0
D . M 1 3 ; 0 ; 0
Chọn A
Gọi 
là một vec tơ pháp tuyến của mặt phẳng (P).
Theo đề bài ta có mặt phẳng (P) vuông góc với mặt phẳng (α): x-y+z-4=0 nên ta có phương trình a-b+c=0 ó b=a+c 
Phương trình mặt phẳng (P) đi qua A(0;1;2) và có véc tơ pháp tuyến là ax+ (a+c) (y-1)+c (z-2) =0
Khoảng cách từ tâm I (3;1;2) đến mặt phẳng (P) là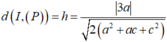 
Gọi r là bán kính của đường tròn giao tuyến giữa mặt cầu (S) và mặt phẳng (P) ta có r²=16-h² ; r nhỏ nhất khi h lớn nhất.
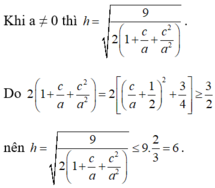
Dấu “=” xảy ra khi a = -2c. => một véc tơ pháp tuyến là 
=> phương trình mặt phẳng (P) là 2x+y-z+1=0.
Vậy tọa độ giao điểm M của (P) và trục x'Ox là: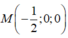 
Đúng 0
Bình luận (0)
Trong không gian Oxyz, cho điểm
A
(
0
;
1
;
2
)
, mặt phẳng
α
:
x
-
y
+
z
-
4
0
và mặt cầu
S
:
(
x
-
3...
Đọc tiếp
Trong không gian Oxyz, cho điểm A ( 0 ; 1 ; 2 ) , mặt phẳng α : x - y + z - 4 = 0 và mặt cầu S : ( x - 3 ) 2 + ( y - 1 ) 2 + ( z - 2 ) 2 = 16 . Gọi (P) là mặt phẳng đi qua A, vuông góc với α và đồng thời (P) cắt mặt cầu (S) theo giao tuyến là một đường tròn có bán kính nhỏ nhất. Tọa độ giao điểm M của (P) và trục x'Ox là:
Trong không gian Oxyz cho mặt phẳng (P): 5x+my+4z+n0 đi qua giao tuyến của hai mặt phẳng
α
: 3x-7y+z-30 và
β
: x-9y-2z+50. Tính m+n A. 6 B. -16 C. -3 D. -4
Đọc tiếp
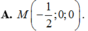
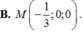
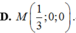
Trong không gian Oxyz cho mặt phẳng (P): 5x+my+4z+n=0 đi qua giao tuyến của hai mặt phẳng α : 3x-7y+z-3=0 và β : x-9y-2z+5=0. Tính m+n
A. 6
B. -16
C. -3
D. -4
Trong không gian với hệ tọa độ Oxyz, cho điểm A(0;1;2), mặt phẳng
α
:
x
-
y
+
z
0
và
S
:
x
-
3
2
+
y
-
1
2
+...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho điểm A(0;1;2), mặt phẳng α : x - y + z = 0 và S : x - 3 2 + y - 1 2 + z - 2 2 = 16 . Gọi (P) là mặt phẳng đi qua A, vuông góc với α và đồng thời (P) cắt mặt cầu (S) theo giao tuyến là một đường tròn có bán kính nhỏ nhất. Tọa độ giao điểm M của (P) và trục xOx' là
A. M - 1 3 ; 0 ; 0
B. M(1;0;0)
C. M - 1 2 ; 0 ; 0
D. M 1 3 ; 0 ; 0
Trong không gian Oxyz cho mặt cầu (S):
(
x
-
1
)
2
+
(
y
+
2
)
2
+
(
z
-
3
)
2...
Đọc tiếp
Trong không gian Oxyz cho mặt cầu (S): ( x - 1 ) 2 + ( y + 2 ) 2 + ( z - 3 ) 2 = 27 . Gọi ( α ) là mặt phẳng đi qua hai điểm A(0;0;-4), B(2;0;0) và cắt (S) theo giao tuyến là đường tròn (C) sao cho khối nón có đỉnh là tâm của (S), đáy là (C) có thể tích lớn nhất. Biết mặt phẳng ( α ) có phương trình dạng ax+by-z+c= 0, khi đó a-b+c bằng:
A. -4.
B. 8
C. 0
D. 2
Trong không gian Oxyz, cho mặt cầu (S): (x-1)²+ (y+2)²+ (z-3)²27. Gọi (α) là mặt phẳng đi qua hai điểm A (0; 0; -4), B (2; 0; 0) và cắt (S) theo giao tuyến là đường tròn (C) sao cho khối nón đỉnh là tâm của (S) và đáy là là đường tròn (C) có thể tích lớn nhất. Biết rằng (α): ax+by-z+c0, khi đó a-b+c bằng: A. -4. B. 8. C. 0. D. 2.
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu (S): (x-1)²+ (y+2)²+ (z-3)²=27. Gọi (α) là mặt phẳng đi qua hai điểm A (0; 0; -4), B (2; 0; 0) và cắt (S) theo giao tuyến là đường tròn (C) sao cho khối nón đỉnh là tâm của (S) và đáy là là đường tròn (C) có thể tích lớn nhất. Biết rằng (α): ax+by-z+c=0, khi đó a-b+c bằng:
A. -4.
B. 8.
C. 0.
D. 2.
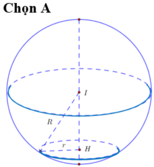
Mặt cầu (S) có tâm I (1;-2;3) và bán kính R= 3√3.
Vì (α): ax+by-z+c=0 đi qua hai điểm A (0; 0; -4), B (2; 0; 0) nên c = -4 và a = 2.
Suy ra (α): 2x+by-z-4=0.
Đặt IH = x, với 0 < x < 3√3 ta có 
Thể tích khối nón là
Đúng 0
Bình luận (0)