Cho hàm số f x = 12 x ≥ 9 a x − 2 b − 12 x − 1 3 − 2 x < 9 . Biết rằng a, b là giá trị thực để hàm số liên tục tại x 0 = 9. Tính giá trị của P = a + b
A. P = 1 2
B. P = 5
C. P = 17
D. P = − 1 2
PB
Những câu hỏi liên quan
Cho hàm số f(x) có đạo hàm f'(x) = x 2 - 1 2 (x-5)(x+2). Số điểm cực trị của hàm số f(x) bằng:
A. 4
B. 3
C. 1
D. 2
Chọn D
Từ giả thiết ta có:
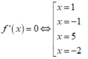
Từ bảng biến thiên ta thấy f'(x) đổi dấu tại x = -2 và x = 5 do đó hàm số f(x) có 2 điểm cực trị.
Đúng 0
Bình luận (0)
Cho hàm số f(x) có đạo hàm
f
(
x
)
x
x
+
1
2
. Hàm số đồng biến trên khoảng nào dưới đây? A.
-
1
;
+
∞
B.
-
1
;...
Đọc tiếp
Cho hàm số f(x) có đạo hàm f ' ( x ) = x x + 1 2 . Hàm số đồng biến trên khoảng nào dưới đây?
A. - 1 ; + ∞
B. - 1 ; 0
C. - ∞ ; - 1
D. 0 ; + ∞
Ta có:
f ' ( x ) = x ( x + 1 ) 2 > 0 ⇔ x > 0
Vậy hàm số đã cho đồng biến trên 0 ; + ∞
Chọn đáp án D.
Đúng 0
Bình luận (0)
Cho hàm số y f(x) có đạo hàm f(x)
(
e
x
+
1
)
(
e
x
-
12
)
(
x
+
1
)
(
x
-
1
)
2
trên R. Hỏi hàm số yf(x) có bao nhiêu điểm cực trị? A. 1. B. 2. C. 3. D. 4.
Đọc tiếp
Cho hàm số y = f(x) có đạo hàm f'(x)= ( e x + 1 ) ( e x - 12 ) ( x + 1 ) ( x - 1 ) 2 trên R. Hỏi hàm số y=f(x) có bao nhiêu điểm cực trị?
A. 1.
B. 2.
C. 3.
D. 4.
Cho hàm số f(x) có đạo hàm
f
(
x
)
x
+
1
2
(
x
-
3
)
.
Mệnh đề nào dưới đây đúng? A. Hàm số đạt cực đại tại x 3 B. Hàm số đạt cực tiểu tại x 3 C. Hàm số đạt cực tiểu tại x -1 D. Hàm số đạt cực đại tại x -1
Đọc tiếp
Cho hàm số f(x) có đạo hàm f ' ( x ) = x + 1 2 ( x - 3 ) . Mệnh đề nào dưới đây đúng?
A. Hàm số đạt cực đại tại x = 3
B. Hàm số đạt cực tiểu tại x = 3
C. Hàm số đạt cực tiểu tại x = -1
D. Hàm số đạt cực đại tại x = -1
Đáp án B
Phương pháp:
Nếu f'(x) đổi dấu khi qua điểm x = x0 ⇒ x = x0 là điểm cực trị của hàm số.
Cách giải:
f'(x) đổi dấu từ - sang + tại x = 3 ⇒ Hàm số đạt cực tiểu tại x = 3
Đúng 0
Bình luận (0)
Cho hàm số yf(x) Đồ thị hàm số yf’(x) như hình bên. Xét hàm số
g
x
2
f
x
-
x
+
1
2
mệnh đề nào sau đây đúng ? A.
m
a
x
-
3
;
3...
Đọc tiếp
Cho hàm số y=f(x) Đồ thị hàm số y=f’(x) như hình bên. Xét hàm số g x = 2 f x - x + 1 2 mệnh đề nào sau đây đúng ?
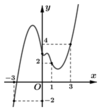
A. m a x - 3 ; 3 g x = g 1
B. m a x - 3 ; 3 g x = g 3
C. m i n - 3 ; 3 g x = g 1
D. Không tồn tại giá trị nhỏ nhất của g(x) trên [3;3]
Ta có 
Suy ra số nghiệm của phương trình g’(x) = 0 chính là số giao điểm giữa đồ thị của hàm số y = f’(x) và đường thẳng y = x + 1 Dựa vào đồ thị ta suy ra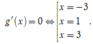 
Bảng biến thiên
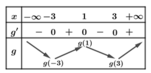
Dựa vào bảng biến thiên, suy ra m a x - 3 ; 3 g x = g 1
Chọn A.
Đúng 0
Bình luận (0)
Cho hàm số yf(x) có đạo hàm f(x)
(
e
x
+
1
)
(
e
x
-
12
)
(
x
+
1
)
(
x
-
1
)
2
trên R. Hỏi hàm số có bao nhiêu điểm cực trị? A. 1. B. 2. C. 3. D. 4.
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm
f'(x)= ( e x + 1 ) ( e x - 12 ) ( x + 1 ) ( x - 1 ) 2 trên R.
Hỏi hàm số 
có bao nhiêu điểm cực trị?
A. 1.
B. 2.
C. 3.
D. 4.
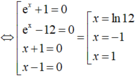
Trong đó ta thấy x=1 là nghiệm bội hai của phương trình ⇒ x=1 không là điểm cực trị của hàm số
Vậy hàm số có 2 điểm cực trị.
Chọn B
Đúng 0
Bình luận (0)
Cho hàm số
f
(
x
)
2
x
2
-
3
x
+
1...
Đọc tiếp
Cho hàm số f ( x ) = 2 x 2 - 3 x + 1 2 ( x - 1 ) k h i x ≠ 1 m k h i x = 1 . Tìm m để hàm số f(x) liên tục tại x=1.
A. 
.
B. 
.
C. 
.
D. 
.
Cho hàm số
f
(
x
)
a
x
4
+
b
x
2
+
c
có
m
i
n
(
-
∞
;
0
)
f
(
x
)
f
(
-
1...
Đọc tiếp
Cho hàm số f ( x ) = a x 4 + b x 2 + c có m i n ( - ∞ ; 0 ) f ( x ) = f ( - 1 ) . Giá trị nhỏ nhất của hàm số y=f(x) trên đoạn [ 1 2 ;2] bằng
A. c + 8a
B. c - 7 16 a
C. c + 9 16 a
D. c - a
Cho hàm số yf(x) có đạo hàm trên R. Đồ thị của hàm số yf(x) như hình vẽ bên. Hàm số
y
g
(
x
)
2
f
(
x
)
-
x
+
1
2
. Mệnh đề nào dưới đây là đúng? A. Hàm số yg(x) đồng biến trên khoảng (1;3) B. Đồ thị hàm số yg(x) có 2 điểm cực trị C. Hàm số yg(x) đạt cực đại tại x1 D. Hàm số...
Đọc tiếp
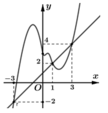
Cho hàm số y=f(x) có đạo hàm trên R. Đồ thị của hàm số y=f(x) như hình vẽ bên. Hàm số y = g ( x ) = 2 f ( x ) - x + 1 2 . Mệnh đề nào dưới đây là đúng?
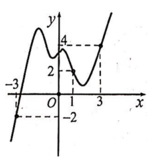
A. Hàm số y=g(x) đồng biến trên khoảng (1;3)
B. Đồ thị hàm số y=g(x) có 2 điểm cực trị
C. Hàm số y=g(x) đạt cực đại tại x=1
D. Hàm số y=g(x) nghịch biến trên khoảng ( 3 ; + ∞ )
Cho hàm số yf(x). Hàm số y f’(x) có đồ thị như hình vẽ dưới đây. Đặt
g
(
x
)
2
f
(
x
)
-
x
+
1
2
.Biết f(-2)f(3). Mệnh đề nào đúng? A. B C. D.
Đọc tiếp
Cho hàm số y=f(x). Hàm số y= f’(x) có đồ thị như hình vẽ dưới đây.
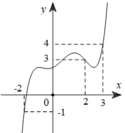
Đặt g ( x ) = 2 f ( x ) - x + 1 2 .Biết f(-2)=f(3). Mệnh đề nào đúng?
A. 
B
C. 
D. 
