Ta có ![]()
Suy ra số nghiệm của phương trình g’(x) = 0 chính là số giao điểm giữa đồ thị của hàm số y = f’(x) và đường thẳng y = x + 1 Dựa vào đồ thị ta suy ra 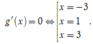
Bảng biến thiên
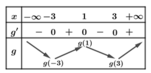
Dựa vào bảng biến thiên, suy ra m a x - 3 ; 3 g x = g 1
Chọn A.

Ta có ![]()
Suy ra số nghiệm của phương trình g’(x) = 0 chính là số giao điểm giữa đồ thị của hàm số y = f’(x) và đường thẳng y = x + 1 Dựa vào đồ thị ta suy ra 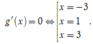
Bảng biến thiên

Dựa vào bảng biến thiên, suy ra m a x - 3 ; 3 g x = g 1
Chọn A.
Cho hàm số y=f(x) có đạo hàm liên tục trên R và có đồ thị hàm số y=f' (x) như hình vẽ bên. Xét hàm số g(x)=f(x^2-3) và các mệnh đề sau:

1. Hàm số g(x) có 3 điểm cực trị.
2. Hàm số g(x)đạt cực tiểu tại x = 0.
3. Hàm số g(x)đạt cực đại tại x = 2.
4. Hàm số g(x)đồng biến trên khoảng (-2;0).
5. Hàm số g(x)nghịch biến trên khoảng (-1;1).
Có bao nhiêu mệnh đề đúng trong các mệnh đề trên?
A. 1.
B. 4.
C. 3.
D. 2.
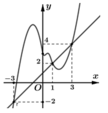
Hàm số y = f(x) có đồ thị y = f'(x) như hình vẽ.
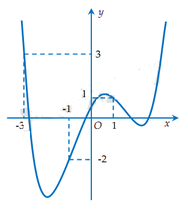
Xét hàm số:
g ( x ) = f ( x ) - 1 3 x 3 - 3 4 x 2 + 3 2 x + 2017
Trong các mệnh đề dưới đây:
(I) g(0) < g(1)
(II) m i n x ∈ - 3 ; 1 g ( x ) = g ( - 1 )
(III) Hàm số g(x) nghịch biến trên (-3;-1)
(IV) m a x x ∈ - 3 ; 1 g ( x ) = m a x g ( - 3 ) , g ( 1 )
Số mệnh đề đúng là:
A. 2
B. 1
C. 3
D. 4
Cho hàm số y = f ( x ) liên tục trên R và có đồ thị hàm số y = f ' ( x ) như hình bên:
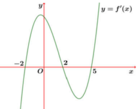
Hỏi hàm số g ( x ) = f ( 3 - 2 x ) nghịch biến trên khoảng nào sau đây?
A. (-1;+∞)
B. (-∞;-1)
C. (1;3)
D. (0;2)
Cho hàm số y = f(x). Đồ thị hàm số y=f '(x) như hình bên dưới.
Hàm số g(x)=f(|3-x|) đồng biến trên khoảng nào trong các khoảng sau?
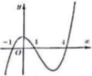
A. (4;7).
B. (2;3).
C. - ∞ ; - 1
D. (-1;2).
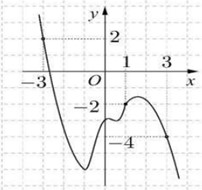
Cho hai hàm số f ( x ) = a x 4 + b x 3 + c x 2 + d x + e với a ≠ 0 và g(x)= p x 2 + q x - 3 c ó đồ thị như hình vẽ bên dưới. Đồ thị hàm số y=f(x) đi qua gốc tọa độ và cắt đồ thị hàm số y=g(x) tại bốn điểm có hoành độ lần lượt là -2;-1;1 và m. Tiếp tuyến của đồ thị hàm số y=f(x)-g(x) tại điểm có hoành độ x=-2 có hệ số góc bằng -15/2. Gọi (H) là hình phẳng giới hạn bởi đồ thị hai hàm số y=f(x) và y=g(x) (phần được tô đậm trong hình vẽ). Diện tích của hình (H) bằng

A. 1553 120
B. 1553 240
C. 1553 60
D. 1553 30
Cho hàm số y=f(x). Đồ thị hàm số y=f'(x) như hình vẽ bên. Đặt g ( x ) = 2 f ( x ) + ( x + 1 ) 2 . Mệnh đề nào dưới đây đúng
A. maxg(x) trên [-3; 3] =g(-3)
B. maxg(x) trên [-3; 3] =g(2)
C. maxg(x) trên [-3; 3] =g(1)
D. maxg(x) trên [-3; 3] =g(-1)
Cho hàm số bậc 3:y=f(x) có đồ thị như hình vẽ.
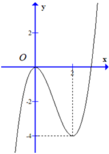
Xét hàm số g(x)=f[(x)]. Trong các mệnh đề dưới đây:
g(x) đồng biến trên (-∞;0) và (2;+∞).
Hàm số g(x) có bốn điểm cực trị.
m a x - 1 ; 1 g x = 0 .
Phương trình g(x)=0 có ba nghiệm.
Số mệnh đề đúng là
A. 3.
B. 2.
C. 1.
D. 4.
Cho hàm số y = f(x) có đạo hàm liên tục trên R. Đường cong trong hình vẽ bên là đồ thị của hàm số y = f’(x). Xét hàm số g(x) = f(x2 – 3). Mệnh đề nào dưới đây sai ?
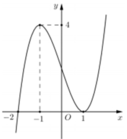
A. Hàm số g(x) đồng biến trên (–1;0)
B. Hàm số g(x) nghịch biến trên (–∞;–1)
C. Hàm số g(x) nghịch biến trên (1;2)
D. Hàm số g(x) đồng biến trên (2;+ ∞)
Cho hàm số y=f(x) có đạo hàm trên R. Hàm số y=f '(x) có đồ thị như hình vẽ bên. Đặt y = g ( x ) = f ( x ) - x 3 3 + x 2 - x + 1 . Khẳng định nào sau đây là đúng?
A. g(1)>g(0)>g(2)
B. g(1)>g(2)>g(0)
C. g(2)>g(0)>g(1)
D. g(0)>g(2)>g(1)