Đáp án C

Gọi G là trọng tâm tam giác ABC.

Vì tứ diện ABCD đều nên A G ⊥ ( B C D ) .

Ta có  C D ⊥ A G C D ⊥ B G

Vậy số đo góc giữa hai đường thẳng AB và CD bằng 90⁰.

Đáp án D

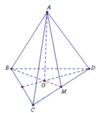
Gọi M là trung điểm CD

C D ⊥ B M C D ⊥ A M ⇒ C D ⊥ A B M ⇒ C D ⊥ A B C D ; A B = 90 °

(góc nội tiếp chắn cung BCD) (1)

( góc nội tiếp chắn cung ABC) (2)

Từ (1) và (2) có:

(3)

và là hai góc trong cùng phía tạo bởi cát tuyến AD và hai đường thẳng AB, CD.

Đẳng thức (3) chứng tỏ AB // CD. Do đó tứ giác ABCD là hình thang, mà hình thang nội tiếp là hình thang cân.

Vậy ABCD là hình thang cân (BC = AD và sđ cung BC = AD = 90^o )

b) Giả sử hai đường chéo AC và BD cắt nhau tại I.

là góc có đỉnh nằm trong đường tròn, nên:

Vậy AC ⊥ BD

c)

Vì sđ cung AB = 60^o nên => ∆AIB đều, nên AB = R

Vì sđ cung BC = 90^o nên BC = R√2

AD = BC = R√2

nên sđ cung CD= 120^o nên CD = R√3

Hướng dẫn giải:

(góc nội tiếp chắn cung BCD) (1)

( góc nội tiếp chắn cung ABC) (2)

Từ (1) và (2) có:

(3)

và là hai góc trong cùng phía tạo bởi cát tuyến AD và hai đường thẳng AB, CD.

Đẳng thức (3) chứng tỏ AB // CD. Do đó tứ giác ABCD là hình thang, mà hình thang nội tiếp là hình thang cân.

Vậy ABCD là hình thang cân (BC = AD và sđ cung BC = AD = 90^o )

b) Giả sử hai đường chéo AC và BD cắt nhau tại I.

là góc có đỉnh nằm trong đường tròn, nên:

Vậy AC ⊥ BD

c)

Vì sđ cung AB = 60^o nên => ∆AIB đều, nên AB = R

Vì sđ cung BC = 90^o nên BC = R√2

AD = BC = R√2

nên sđ cung CD= 120^o nên CD = R√3

Đáp án B

Phương pháp giải:  Tứ diện đều có cặp cạnh đối vuông góc với nhau

Lời giải:

Gọi M là trung điểm của CD. Hai tam giác ACD, BCD đều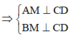 

Vậy góc giữa hai đường thẳng AB và CD bằng 90⁰