Cho a>0,a≠1,b>0,b≠1 thỏa mãn các điều kiện l o g a 1 2017 < l o g a 1 2018 v à b 1 2017 > b 1 2018 . Gía trị lớn nhất của biểu thức P = - l o g a 2 b - l o g a b + l o g a 2 . l o g b 2 - 2 l o g a 2 + 2 là
A. 3
B. 5/2
C. 7/2
D. 4
cho a,b,c khác 0 thỏa mãn điều kiện 1/a+1/b+1/c = 1/ a+b+c
CMR: 1/a2017+1/b2017+ 1/c2017=1/a2017+b2017+c2017
1)cho 3 số x, y,z thỏa mãn điều kiện x+y+z=2018 và x^3+y^3+z^3=2018^3. Cmr (x+y+z)^3=x^2017+y^2017+z^2017
2)
tìm các cặp số nguyên (x y) biết x^2-4xy+5y^2-16=0
3)Cho 3 số a,b,c thỏa mãn a+b+c=0 và a^2+b^2+c^2=2018
4)tính giả trị biểu thức A=a^4+b^4+c^4
cho a > 0; b > 0 thỏa mãn điều kiện a*b =1. CMR:
( a+1)*( b+1) >=1
\(\left(a+1\right)\left(b+1\right)\ge1\)
\(=>ab+a+b+1\ge1\)
\(=>1+a+b+1\ge1\)( luôn đúng ) (* )
KL : (* ) (đúng ) => \(\left(a+1\right)\left(b+1\right)\ge1\)(đúng )
KL
cho a, b là các số thỏa mãn điều kiện: a^2 + b^4 = 1; a^2008 + b^2009 = 0. Tìm các cặp số a, b
Cho a,b,c # 0 và a+b+c#0 thỏa mãn 1/a+1/b+1/c=1/a+b+c cmr 1/a^2017+1/b^2017+1/c^2017=1/a^2017+b^2017+c^2017
Lời giải:
$\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=\frac{1}{a+b+c}$
$\Leftrightarrow (\frac{1}{a}+\frac{1}{b})+(\frac{1}{c}-\frac{1}{a+b+c})=0$
$\Leftrightarrow \frac{a+b}{ab}+\frac{a+b}{c(a+b+c)}=0$
$\Leftrightarrow (a+b)(\frac{1}{ab}+\frac{1}{c(a+b+c)})=0$
$\Leftrightarrow (a+b).\frac{ab+c(a+b+c)}{abc(a+b+c)}=0$
$\Leftrightarrow \frac{(a+b)(c+a)(c+b)}{abc(a+b+c)}=0$
$\Leftrightarrow (a+b)(c+a)(c+b)=0$
$\Leftrightarrow a+b=0$ hoặc $c+a=0$ hoặc $c+b=0$
Không mất tổng quát giả sử $a+b=0$
$\Leftrightarrow a=-b$.
Khi đó:
$\frac{1}{a^{2017}}+\frac{1}{b^{2017}}+\frac{1}{c^{2017}}=\frac{1}{(-b)^{2017}}+\frac{1}{b^{2017}}+\frac{1}{c^{2017}}$
$=\frac{-1}{b^{2017}}+\frac{1}{b^{2017}}+\frac{1}{c^{2017}}$
$=\frac{1}{c^{2017}}=\frac{1}{(-b)^{2017}+b^{2017}+c^{2017}}$
$=\frac{1}{a^{2017}+b^{2017}+c^{2017}}$ (đpcm)
Lần sau bạn lưu ghi đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) để được hỗ trợ tốt nhất. Mọi người đọc đề của bạn dễ hiểu thì cũng sẽ dễ giúp hơn.
Cho 0 < a ≠ 1 , b > 0 thỏa mãn điều kiện log a b < 0 . Khẳng định nào sau đây là đúng
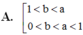
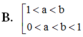
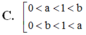
![]()
Cho 0 < a ≠ 1 , b > 0 thỏa mãn điều kiện log a b < 0. Khẳng định nào sau đây là đúng
A. 1 < b < a 0 < b < a < 1
B. 1 < a < b 0 < a < b < 1
C. 0 < a < 1 < b 0 < b < 1 < a
D. 0 < b < 1 ≤ a
Đáp án C
Ta có log a b < 0 ⇔ log a b < log a 1. Xét 2 trường hợp
T H 1 : a > 1 suy ra log a b < log a 1 ⇔ b < 1. Kết hợp điều kiện ta được 0 < b < 1 < a
T H 2 : 0 < a < 1 suy ra log a b < log a 1 ⇔ b > 1. Kết hợp điều kiện ta được 0 < a < 1 < b
Vậy khẳng định đúng là 0 < a < 1 < b 0 < b < 1 < a
cho a,b,c khác 0 thỏa mãn a^2017 b^2017 c^2017=1; a^2(b c) b^2(c a) c^2(a b) 2abc =0 tính 1/a^2017 1/b^2017 1/c^2017
Cho a,b,c thỏa mãn điều kiện ab + bc + ca = abc avf a + b + c = 1 . CMR : (a-1)(b-1)(c-1) = 0